 |
|
Firstly, we cannot hope to introduce finite state transducers and how they are used in speech recognition.
For that, see "Speech Recognition with Weighted Finite-State Transducers" by Mohri, Pereira and Riley (in Springer Handbook on SpeechProcessing and Speech Communication, 2008). The general approach we use is as described there, but some of the details, particularly with respect to how we handle disambiguation symbols and how we deal with weight-pushing, differ.
The overall picture for decoding-graph creation is that we are constructing the graph HCLG = H o C o L o G. Here
This is the standard recipe. However, there are a lot of details to be filled in. We want to ensure that the output is determinized and minimized, and in order for HCLG to be determinizable we have to insert disambiguation symbols. For details on the disambiguation symbols, see below Disambiguation symbols.
We also want to ensure the HCLG is stochastic, as far as possible; in the conventional recipes, this is done (if at all) with the "push-weights" operation. Our approach to ensuring stochasticity is different, and is based on ensuring that no graph creation step "takes away" stochasticity; see Preserving stochasticity and testing it for details.
If we were to summarize our approach on one line (and one line can't capture all the details, obviously), the line would probably as follows, where asl=="add-self-loops" and rds=="remove-disambiguation-symbols", and H' is H without the self-loops:
HCLG = asl(min(rds(det(H' o min(det(C o min(det(L o G))))))))
Weight-pushing is not part of the recipe; instead we aim to ensure that no stage of graph creation will stop the result from being stochastic, as long as G was stochastic. Of course, G will typically not be quite stochastic, because of the way Arpa language models with backoff are represented in FSTs, but at least our approach ensures that the non-stochasticity "stays put" and does not get worse than it was at the start; this approach avoids the danger of the "push-weights" operation failing or making things worse.
Disambiguation symbols are the symbols #1, #2, #3 and so on that are inserted at the end of phonemene sequences in the lexicon. When a phoneme sequence is a prefix of another phoneme sequence in the lexicon, or appears in more than one word, it needs to have one of these symbols added after it. These symbols are needed to ensure that the product L o G is determinizable. We also insert disambiguation symbols in two more places. We have a symbol #0 on the backoff arcs in the language model G; this ensures that G is determinizable after removing epsilons (since our determinization algorithm does remove epsilons). We also have a symbol #-1 in place of epsilons that appear on the left of context FST C, at the beginning of the utterance (before we start outputting symbols). This is necessary to fix a rather subtle problem that happens when we have words with an empty phonetic representation (e.g. the beginning and end of sentence symbols <s> and </s>).
We give the outline of how we would formally prove that the intermediate stages of graph compilation (e.g. LG, CLG, HCLG) are determinizable; this is important in ensuring that our recipe never fails. By determinizable, we mean determinizable after epsilon removal. The general setup is: first, we stipulate that G must be determinizable. This is why we need the #0 symbols (G is actually deterministic, hence determinizable). Then we want L to be such that for any determinizable G, L o G is determinizable. [The same goes for C, with L o G on the right instead of G]. There are a lot of details of the theory still to be fleshed out, but I believe it is sufficient for L to have two properties:
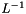must be functionalThe same applies of course to the C transducer. We believe that the transducers as our scripts and programs currently create them have these properties.
The ContextFst object (C) is a dynamically created FST object that represents a transducer from context-dependent phones to context-independent phones. The purpose of this object is to avoid us having to enumerate all possible phones in context, which could be difficult when the context width (N) or the number of phones is larger than normal. The constructor ContextFst::ContextFst requires the context-width (N) and central-position (P) which are further explained in Phonetic context windows; their normal values corresponding to a triphone system are 3 and 1, respectively. It also requires the integer id of a special symbol, the "subsequential symbol" (referred to as '$' in the reference given above), which the FST outputs N-P-1 times after all phones are seen (this ensures that the context FST is output-deterministic). In addition to this it requires lists of the integer id's of the phones and the disambiguation symbols. The vocabulary on the output side of the ContextFst consists of the set of phones and disambiguation symbols plus the subsequential symbol. The vocabulary on the input side is dynamically generated and (apart from epsilon, which is not used), corresponds to phones in context, disambiguation symbols, and a special symbol that we write as #-1 that takes the place of epsilon in the "traditional recipe", but which we treat as any other disambiguation symbol (it is necessary to ensure determinizability in the sense we prefer, i.e. with epsilon removal). The subsequential symbol '$' has nothing corresponding to it on the input side (this is also the case in the traditional recipe). The symbol id's corresponding to the disambiguation symbols on the input side are not necessarily the same integer identifiers as used on the output side for the corresponding symbols. The ContextFst object has a function ILabelInfo() which returns a reference to an object of type std::vector<std::vector<int32> > which enables the user to work out the "meaning" of each symbol on the input side. The correct interpretation of this object is described further in The ilabel_info object.
There is a special "Matcher" object called ContextMatcher which is intended to be used in composition algorithms involving the ContextFst (a Matcher is something that OpenFst's composition algorithm uses for arc lookup; for more explanation, see the OpenFst documentation; ). The ContextMatcher makes the use of the ContextFst object more efficient, by avoiding the allocation of more states than is necessary (the issue is that with the normal matcher, every time we want any arc out of a state, we would have to allocate the destination states of all other arcs out of that state). There is an associated function, ComposeContextFst(), which performs FST composition in the case where the left hand argument to composition is of type ContxtFst; it uses this matcher. There is also a function ComposeContext(), which is similar but creates the ContextFst object itself.
We deal with the whole question of weight pushing in a slightly different way from the traditional recipe. Weight pushing in the log semiring can be helpful in speeding up search (weight pushing is an FST operation that ensures that the arc probabilities out of each state "sum to one" in the appropriate sense). However, in some cases weight pushing can have bad effects. The issue is that statistical language models, when represented as FSTs, generally "add up to more than one" because some words are counted twice (directly, and via backoff arcs).
We decided to avoid ever pushing weights, so instead we handle the whole issue in a different way. Firstly, a definition: we call a "stochastic" FST one whose weights sum to one, and the reader can assume that we are talking about the log semiring here, not the tropical one, so that "sum to one" really means sum, and not "take the max". We ensure that each stage of graph creation has the property that if the previous stage was stochastic, then the next stage will be stochastic. That is: if G is stochastic, then LG will be stochastic; if LG is stochastic, then det(LG) will be stochastic; if det(LG) is stochastic, then min(det(LG)) will be stochastic, and so on and so forth. This means that each individual operation must, in the appropriate sense, "preserve stochasticity". Now, it would be quite possible to do this in a very trivial but not-very-useful way: for instance, we could just try the push-weights algorithm and if it seems to be failing because, say, the original G fst summed up to more than one, then we throw up our hands in horror and announce failure. This would not be very helpful.
We want to preserve stochasticity in a stronger sense, which is to say: first measure, for G, the min and max over all its states, of the sum of the (arc probabilities plus final-prob) out of those states. This is what our program "fstisstochastic" does. If G is stochastic, both of these numbers would be one (you would actually see zeros from the program, because actually we operate in log space; this is what "log semiring" means). We want to preserve stochasticity in the following sense: that this min and max never "get worse"; that is, they never get farther away from one. In fact, this is what naturally happens when we have algorithms that preserve stochasticity in a "local" way. There are various algorithms that we need to preserve stochasticity, including:
These properties are true of C, L and H, at least if everything is properly normalized (i.e. if the lexicon weights sum to one for any given word, and if the HMMs in H are properly normalized and we don't use a probability scale). However, in practice in our graph creation recipes we use a probability scale on the transition probabilities in the HMMs (similar to the acoustic scale). This means that the very last stages of graph creation typically don't preserve stochasticity. Also, if we are using a statistical language model, G will typically not be stochastic in the first place. What we do in this case is we measure at the start how much it "deviates from stochasticity" (using the program fstisstochastic), and during subsequent graph creation stages (except for the very last one) we verify that the non-stochasticity does not "get worse" than it was at the beginning.
1.8.13