#include <compressed-transform-stats.h>

Collaboration diagram for CompressedAffineXformStats:

[legend]

Public Member Functions
	CompressedAffineXformStats ()

	CompressedAffineXformStats (const AffineXformStats &input)

void	CopyFromAffineXformStats (const AffineXformStats &input)

void	CopyToAffineXformStats (AffineXformStats *output) const

void	Write (std::ostream &os, bool binary) const

void	Read (std::istream &is, bool binary)

Static Private Member Functions
static void	PrepareOneG (const SpMatrix< double > &Gi, double beta, SubVector< double > *linearized)

static void	ExtractOneG (const SubVector< double > &linearized, double beta, SpMatrix< double > *Gi)

Private Attributes
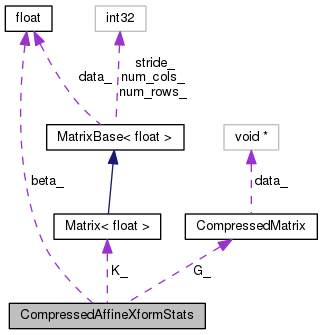
float	beta_

Matrix< float >	K_

CompressedMatrix	G_

Detailed Description

Definition at line 44 of file compressed-transform-stats.h.

Constructor & Destructor Documentation

◆ CompressedAffineXformStats() [1/2]

CompressedAffineXformStats ( )

inline

Definition at line 46 of file compressed-transform-stats.h.

46 : beta_(0.0) { }

kaldi::CompressedAffineXformStats::beta_

float beta_

Definition: compressed-transform-stats.h:62

◆ CompressedAffineXformStats() [2/2]

CompressedAffineXformStats ( const AffineXformStats & input )

inline

Definition at line 47 of file compressed-transform-stats.h.

References CompressedAffineXformStats::CopyFromAffineXformStats(), CompressedAffineXformStats::CopyToAffineXformStats(), CompressedAffineXformStats::Read(), and CompressedAffineXformStats::Write().

                                                             {
     CopyFromAffineXformStats(input);
   }

Member Function Documentation

◆ CopyFromAffineXformStats()

void CopyFromAffineXformStats ( const AffineXformStats & input )

Definition at line 28 of file compressed-transform-stats.cc.

References VectorBase< Real >::AddVec(), AffineXformStats::beta_, CompressedAffineXformStats::beta_, CompressedMatrix::CopyFromMat(), MatrixBase< Real >::CopyFromMat(), VectorBase< Real >::CopyRowFromSp(), AffineXformStats::Dim(), CompressedAffineXformStats::ExtractOneG(), AffineXformStats::G_, CompressedAffineXformStats::G_, rnnlm::i, AffineXformStats::K_, CompressedAffineXformStats::K_, KALDI_ASSERT, MatrixBase< Real >::NumCols(), MatrixBase< Real >::NumRows(), CompressedAffineXformStats::PrepareOneG(), and Matrix< Real >::Resize().

Referenced by CompressedAffineXformStats::CompressedAffineXformStats().

                                    {
   int32 dim = input.Dim();
   beta_ = input.beta_;
   if (beta_ == 0.0) { // empty; no stats.
     K_.Resize(dim, dim+1); // Will set to zero.
     // This stores the dimension.  Inefficient but this shouldn't happen often.
     Matrix<float> empty;
     G_.CopyFromMat(empty); // Sets G empty.
     return;
   }
   KALDI_ASSERT(input.G_.size() == dim && input.K_.NumCols() == dim+1
                && input.K_.NumRows() == dim && input.G_[0].NumRows() == dim+1);
   // OK, we have valid, nonempty stats.
   // We first slightly change the format of G.
   Matrix<double> Gtmp(dim, 1 + (((dim+1)*(dim+2))/2));
   // Gtmp will be compressed into G_.  The first element of each
   // row of Gtmp is the trace of the corresponding G[i], divided
   // by (beta * dim).  [this division is so we expect it to be
   // approximately 1, to keep things in a good range so they
   // can be more easily compressed.]  The next (((dim+1)*(dim+2))/2))
   // elements are the linearized form of the symmetric (d+1) by (d+1) matrix
   // input.G_[i], normalized appropriately using that trace.
 
   Matrix<double> K_corrected(input.K_); // This K_corrected matrix is a version of the
   // K_ matrix that we will correct to ensure that the derivative of the
   // objective function around the default matrix stays the same after
   // compression.
 
   SpMatrix<double> Gi_tmp(dim+1);
   for (int32 i = 0; i < dim; i++) {
     SubVector<double> this_row(Gtmp, i);
     PrepareOneG(input.G_[i], beta_, &this_row);
     ExtractOneG(this_row, beta_, &Gi_tmp);
 
     // At this stage we use the difference betwen Gi and Gi_tmp to
     // make a correction to K_.
     Vector<double> old_g_row(dim+1), new_g_row(dim+1);
     old_g_row.CopyRowFromSp(input.G_[i], i); // i'th row of old G_i.
     new_g_row.CopyRowFromSp(Gi_tmp, i); // i'th row of compressed+reconstructed G_i.
     // The auxiliary function for the i'th row of the transform, v_i, is as follows
     // [ignoring the determinant], where/ k_i is the i'th row of K:
     //  v_i . k_i - 0.5 v_i^T G_i u_i.
     // Let u_i be the unit vector in the i'th dimension.  This is the "default" value
     // of v_i.  The derivative of the auxf w.r.t. v_i, taken around this point, is:
     // k_i - G_i u_i
     // which is the same as k_i minus the i'th row (or column) of G_i
     // we want the derivative to be unchanged after compression:
     // new_ki - new_G_i u_i = old_ki - old_G_i u_i
     // new_ki = old_ki - old_G_i u_i + new_G_i u_i.
     // new_ki = old_ki - (i'th row of old G_i) + (i'th row of new G_i).
     
     SubVector<double> Ki(K_corrected, i);
     Ki.AddVec(-1.0, old_g_row);
     Ki.AddVec(+1.0, new_g_row);
   }
   K_.Resize(dim, dim+1);
   K_.CopyFromMat(K_corrected);
   G_.CopyFromMat(Gtmp);
 }

◆ CopyToAffineXformStats()

void CopyToAffineXformStats ( AffineXformStats * output ) const

Definition at line 89 of file compressed-transform-stats.cc.

References AffineXformStats::beta_, CompressedAffineXformStats::beta_, MatrixBase< Real >::CopyFromMat(), CompressedMatrix::CopyToMat(), AffineXformStats::Dim(), CompressedAffineXformStats::ExtractOneG(), AffineXformStats::G_, CompressedAffineXformStats::G_, rnnlm::i, AffineXformStats::Init(), AffineXformStats::K_, CompressedAffineXformStats::K_, CompressedMatrix::NumCols(), MatrixBase< Real >::NumRows(), and CompressedMatrix::NumRows().

Referenced by CompressedAffineXformStats::CompressedAffineXformStats().

                                     {
   int32 dim = K_.NumRows();
   if (dim == 0) {
     output->Init(0, 0);
     return;
   }
   if (output->Dim() != dim || output->G_.size() != dim || beta_ == 0.0)
     output->Init(dim, dim);
   if (beta_ == 0.0) return; // Init() will have cleared it.
   output->beta_ = beta_;
   output->K_.CopyFromMat(K_);
   Matrix<double> Gtmp(G_.NumRows(), G_.NumCols());  // CopyToMat no longer
   // resizes, we have to provide correctly-sized matrix
   G_.CopyToMat(&Gtmp);
   for (int32 i = 0; i < dim; i++) {
     SubVector<double> this_row(Gtmp, i);
     ExtractOneG(this_row, beta_, &(output->G_[i]));
   }
 }

◆ ExtractOneG()

void ExtractOneG	(	const SubVector< double > &	linearized,
		double	beta,
		SpMatrix< double > *	Gi
	)

staticprivate

Definition at line 147 of file compressed-transform-stats.cc.

References SpMatrix< Real >::AddTp2(), PackedMatrix< Real >::CopyFromVec(), KALDI_ASSERT, kaldi::kNoTrans, PackedMatrix< Real >::NumRows(), and VectorBase< Real >::Range().

Referenced by CompressedAffineXformStats::CopyFromAffineXformStats(), and CompressedAffineXformStats::CopyToAffineXformStats().

                                                                    {
   int32 dim = Gi->NumRows() - 1;
   KALDI_ASSERT(dim > 0);
   double norm_trace = linearized(0);
   double raw_trace = norm_trace * beta * dim;
   TpMatrix<double> C(dim+1);
   C.CopyFromVec(linearized.Range(1, ((dim+1)*(dim+2))/2));
   Gi->AddTp2(raw_trace / dim, C, kNoTrans, 0.0);
 }

◆ PrepareOneG()

void PrepareOneG	(	const SpMatrix< double > &	Gi,
		double	beta,
		SubVector< double > *	linearized
	)

staticprivate

Definition at line 128 of file compressed-transform-stats.cc.

References TpMatrix< Real >::Cholesky(), KALDI_ASSERT, PackedMatrix< Real >::NumRows(), PackedMatrix< Real >::Scale(), and SpMatrix< Real >::Trace().

Referenced by CompressedAffineXformStats::CopyFromAffineXformStats().

                                                                             {
   KALDI_ASSERT(beta != 0.0);
   int32 dim = Gi.NumRows() - 1;
   double raw_trace = Gi.Trace();
   double norm_trace = (raw_trace / (beta * dim));
   (*linearized)(0) = norm_trace; // should be around 1.
   SubVector<double> linearized_matrix((*linearized), 1, ((dim+1)*(dim+2))/2);
   TpMatrix<double> C(dim+1);
   C.Cholesky(Gi); // Get the Cholesky factor: after we compress and uncompress
   // this and re-create Gi, it's bound to be +ve semidefinite, which is a Good Thing.
   C.Scale(sqrt(dim / raw_trace)); // This is the scaling that is equivalent
   // to scaling Gi by dim / raw_trace, which would make the diagonals
   // of Gi average to 1.  We can reverse this when we decompress.
   linearized_matrix.CopyFromPacked(C);  
 }

◆ Read()

void Read	(	std::istream &	is,
		bool	binary
	)

Definition at line 118 of file compressed-transform-stats.cc.

References CompressedAffineXformStats::beta_, kaldi::ExpectToken(), CompressedAffineXformStats::G_, CompressedAffineXformStats::K_, CompressedMatrix::Read(), Matrix< Real >::Read(), and kaldi::ReadBasicType().

Referenced by CompressedAffineXformStats::CompressedAffineXformStats().

                                                                  {
   ExpectToken(is, binary, "<CompressedAffineXformStats>");
   ReadBasicType(is, binary, &beta_);
   K_.Read(is, binary);
   G_.Read(is, binary);
   ExpectToken(is, binary, "</CompressedAffineXformStats>");
 }

◆ Write()

void Write	(	std::ostream &	os,
		bool	binary
	)		const

Definition at line 110 of file compressed-transform-stats.cc.

References CompressedAffineXformStats::beta_, CompressedAffineXformStats::G_, CompressedAffineXformStats::K_, CompressedMatrix::Write(), MatrixBase< Real >::Write(), kaldi::WriteBasicType(), and kaldi::WriteToken().

Referenced by CompressedAffineXformStats::CompressedAffineXformStats().

                                                                         {
   WriteToken(os, binary, "<CompressedAffineXformStats>");
   WriteBasicType(os, binary, beta_);
   K_.Write(os, binary);
   G_.Write(os, binary);
   WriteToken(os, binary, "</CompressedAffineXformStats>");
 }