OptimizeLbfgs< Real > Class Template Reference

#include <optimization.h>

Collaboration diagram for OptimizeLbfgs< Real >:

Public Member Functions
	OptimizeLbfgs (const VectorBase< Real > &x, const LbfgsOptions &opts)
	Initializer takes the starting value of x. More...
const VectorBase< Real > &	GetValue (Real *objf_value=NULL) const
	This returns the value of the variable x that has the best objective function so far, and the corresponding objective function value if requested. More...
const VectorBase< Real > &	GetProposedValue () const
	This returns the value at which the function wants us to compute the objective function and gradient. More...
Real	RecentStepLength () const
	Returns the average magnitude of the last n steps (but not more than the number we have stored). More...
void	DoStep (Real function_value, const VectorBase< Real > &gradient)
	The user calls this function to provide the class with the function and gradient info at the point GetProposedValue(). More...
void	DoStep (Real function_value, const VectorBase< Real > &gradient, const VectorBase< Real > &diag_approx_2nd_deriv)
	The user can call this version of DoStep() if it is desired to set some kind of approximate Hessian on this iteration. More...

Private Types
enum	ComputationState { kBeforeStep, kWithinStep }
	"compute p_k <-- - H_k \delta f_k" (i.e. Algorithm 7.4). More...
enum	{ kWolfeI, kWolfeII, kNone }

Private Member Functions
	KALDI_DISALLOW_COPY_AND_ASSIGN (OptimizeLbfgs)
MatrixIndexT	Dim ()
MatrixIndexT	M ()
SubVector< Real >	Y (MatrixIndexT i)
SubVector< Real >	S (MatrixIndexT i)
bool	AcceptStep (Real function_value, const VectorBase< Real > &gradient)
void	Restart (const VectorBase< Real > &x, Real function_value, const VectorBase< Real > &gradient)
void	ComputeNewDirection (Real function_value, const VectorBase< Real > &gradient)
void	ComputeHifNeeded (const VectorBase< Real > &gradient)
void	StepSizeIteration (Real function_value, const VectorBase< Real > &gradient)
void	RecordStepLength (Real s)

Private Attributes
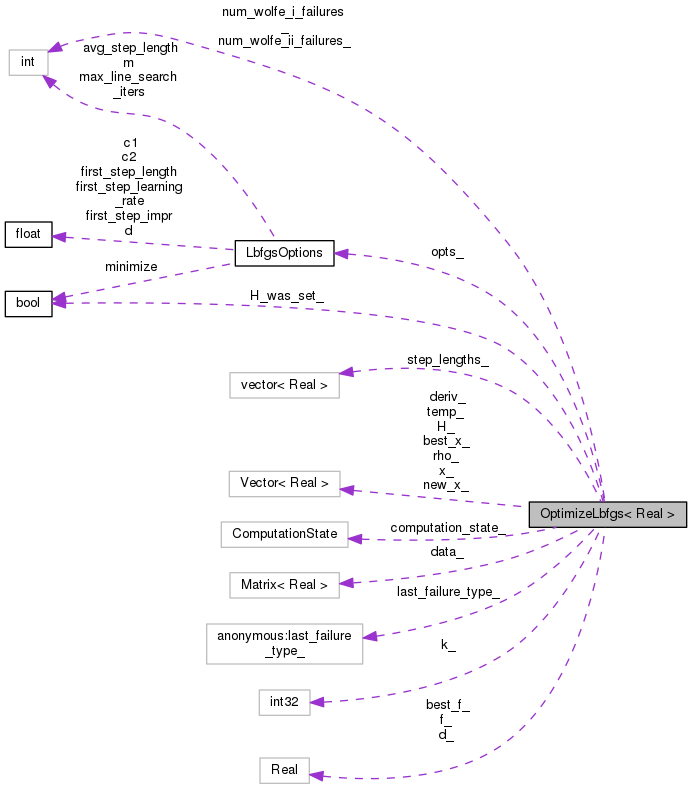
LbfgsOptions	opts_
SignedMatrixIndexT	k_
ComputationState	computation_state_
bool	H_was_set_
Vector< Real >	x_
Vector< Real >	new_x_
Vector< Real >	best_x_
Vector< Real >	deriv_
Vector< Real >	temp_
Real	f_
Real	best_f_
Real	d_
int	num_wolfe_i_failures_
int	num_wolfe_ii_failures_
enum kaldi::OptimizeLbfgs:: { ... }	last_failure_type_
Vector< Real >	H_
Matrix< Real >	data_
Vector< Real >	rho_
std::vector< Real >	step_lengths_

Detailed Description

template<typename Real>
class kaldi::OptimizeLbfgs< Real >

Definition at line 121 of file optimization.h.

Member Enumeration Documentation

anonymous enum

anonymous enum

private

Enumerator
kWolfeI
kWolfeII
kNone

Definition at line 223 of file optimization.h.

{ kWolfeI, kWolfeII, kNone } last_failure_type_; // last type of step-search

ComputationState

enum ComputationState

private

"compute p_k <-- - H_k \delta f_k" (i.e. Algorithm 7.4).

Enumerator
kBeforeStep
kWithinStep

Definition at line 173 of file optimization.h.

                        {
    kBeforeStep,
    kWithinStep, // This means we're within the step-size computation, and
    // have not yet done the 1st function evaluation.
  };

Constructor & Destructor Documentation

OptimizeLbfgs()

OptimizeLbfgs	(	const VectorBase< Real > &	x,
		const LbfgsOptions &	opts
	)

Initializer takes the starting value of x.

Definition at line 35 of file optimization.cc.

References OptimizeLbfgs< Real >::best_f_, OptimizeLbfgs< Real >::best_x_, OptimizeLbfgs< Real >::data_, OptimizeLbfgs< Real >::deriv_, VectorBase< Real >::Dim(), OptimizeLbfgs< Real >::f_, KALDI_ASSERT, LbfgsOptions::m, LbfgsOptions::minimize, OptimizeLbfgs< Real >::new_x_, OptimizeLbfgs< Real >::rho_, OptimizeLbfgs< Real >::temp_, and OptimizeLbfgs< Real >::x_.

                                                            :
    opts_(opts), k_(0), computation_state_(kBeforeStep), H_was_set_(false) {
  KALDI_ASSERT(opts.m > 0); // dimension.
  MatrixIndexT dim = x.Dim();
  KALDI_ASSERT(dim > 0);
  x_ = x; // this is the value of x_k
  new_x_ = x;  // this is where we'll evaluate the function next.
  deriv_.Resize(dim);
  temp_.Resize(dim);
  data_.Resize(2 * opts.m, dim);
  rho_.Resize(opts.m);
  // Just set f_ to some invalid value, as we haven't yet set it.
  f_ = (opts.minimize ? 1 : -1 ) * std::numeric_limits<Real>::infinity();
  best_f_ = f_;
  best_x_ = x_;
}

Member Function Documentation

AcceptStep()

bool AcceptStep ( Real  function_value, const VectorBase< Real > &  gradient  )

private

Definition at line 173 of file optimization.cc.

References VectorBase< Real >::AddVec(), VectorBase< Real >::CopyFromVec(), OptimizeLbfgs< Real >::deriv_, OptimizeLbfgs< Real >::f_, OptimizeLbfgs< Real >::k_, KALDI_VLOG, LbfgsOptions::m, LbfgsOptions::minimize, OptimizeLbfgs< Real >::new_x_, VectorBase< Real >::Norm(), OptimizeLbfgs< Real >::opts_, OptimizeLbfgs< Real >::RecordStepLength(), OptimizeLbfgs< Real >::rho_, OptimizeLbfgs< Real >::S(), kaldi::VecVec(), OptimizeLbfgs< Real >::x_, and OptimizeLbfgs< Real >::Y().

Referenced by OptimizeLbfgs< Real >::StepSizeIteration().

                                                                       {
  // Save s_k = x_{k+1} - x_{k}, and y_k = \nabla f_{k+1} - \nabla f_k.
  SubVector<Real> s = S(k_), y = Y(k_);
  s.CopyFromVec(new_x_);
  s.AddVec(-1.0, x_); // s = new_x_ - x_.
  y.CopyFromVec(gradient);
  y.AddVec(-1.0, deriv_); // y = gradient - deriv_.
  
  // Warning: there is a division in the next line.  This could
  // generate inf or nan, but this wouldn't necessarily be an error
  // at this point because for zero step size or derivative we should
  // terminate the iterations.  But this is up to the calling code.
  Real prod = VecVec(y, s);
  rho_(k_ % opts_.m) = 1.0 / prod;
  Real len = s.Norm(2.0);

  if ((opts_.minimize && prod <= 1.0e-20) || (!opts_.minimize && prod >= -1.0e-20)
      || len == 0.0)
    return false; // This will force restart.
  
  KALDI_VLOG(3) << "Accepted step; length was " << len
                << ", prod was " << prod;
  RecordStepLength(len);
  
  // store x_{k+1} and the function value f_{k+1}.
  x_.CopyFromVec(new_x_);
  f_ = function_value;
  k_++;

  return true; // We successfully accepted the step.
}

ComputeHifNeeded()

void ComputeHifNeeded ( const VectorBase< Real > &  gradient )

private

Definition at line 70 of file optimization.cc.

References LbfgsOptions::first_step_impr, LbfgsOptions::first_step_learning_rate, LbfgsOptions::first_step_length, OptimizeLbfgs< Real >::H_, OptimizeLbfgs< Real >::H_was_set_, OptimizeLbfgs< Real >::k_, KALDI_ASSERT, KALDI_ISINF, KALDI_ISNAN, KALDI_WARN, LbfgsOptions::minimize, VectorBase< Real >::Norm(), OptimizeLbfgs< Real >::opts_, OptimizeLbfgs< Real >::S(), kaldi::VecVec(), OptimizeLbfgs< Real >::x_, and OptimizeLbfgs< Real >::Y().

Referenced by OptimizeLbfgs< Real >::ComputeNewDirection().

                                                                           {
  if (k_ == 0) {
    if (H_.Dim() == 0) {
      // H was never set up.  Set it up for the first time.
      Real learning_rate;
      if (opts_.first_step_length > 0.0) { // this takes
        // precedence over first_step_learning_rate, if set.
        // We are setting up H for the first time.
        Real gradient_length = gradient.Norm(2.0);
        learning_rate = (gradient_length > 0.0 ?
                         opts_.first_step_length / gradient_length :
                         1.0);
      } else if (opts_.first_step_impr > 0.0) {
        Real gradient_length = gradient.Norm(2.0);
        learning_rate = (gradient_length > 0.0 ?
                  opts_.first_step_impr / (gradient_length * gradient_length) :
                  1.0);
      } else {
        learning_rate = opts_.first_step_learning_rate;
      }
      H_.Resize(x_.Dim());
      KALDI_ASSERT(learning_rate > 0.0);
      H_.Set(opts_.minimize ? learning_rate : -learning_rate);
    }
  } else { // k_ > 0
    if (!H_was_set_) { // The user never specified an approximate
      // diagonal inverse Hessian.
      // Set it using formula 7.20: H_k^{(0)} = \gamma_k I, where
      // \gamma_k = s_{k-1}^T y_{k-1} / y_{k-1}^T y_{k-1}
      SubVector<Real> y_km1 = Y(k_-1);
      double gamma_k = VecVec(S(k_-1), y_km1) / VecVec(y_km1, y_km1);
      if (KALDI_ISNAN(gamma_k) || KALDI_ISINF(gamma_k)) {
        KALDI_WARN << "NaN encountered in L-BFGS (already converged?)";
        gamma_k = (opts_.minimize ? 1.0 : -1.0);
      }
      H_.Set(gamma_k);
    }
  }
}  

ComputeNewDirection()

void ComputeNewDirection ( Real  function_value, const VectorBase< Real > &  gradient  )

private

Definition at line 114 of file optimization.cc.

References VectorBase< Real >::AddVec(), VectorBase< Real >::AddVecVec(), OptimizeLbfgs< Real >::computation_state_, OptimizeLbfgs< Real >::ComputeHifNeeded(), LbfgsOptions::d, OptimizeLbfgs< Real >::d_, OptimizeLbfgs< Real >::deriv_, OptimizeLbfgs< Real >::f_, OptimizeLbfgs< Real >::H_, rnnlm::i, OptimizeLbfgs< Real >::k_, KALDI_ASSERT, KALDI_WARN, OptimizeLbfgs< Real >::kBeforeStep, OptimizeLbfgs< Real >::kNone, OptimizeLbfgs< Real >::kWithinStep, OptimizeLbfgs< Real >::last_failure_type_, OptimizeLbfgs< Real >::M(), LbfgsOptions::minimize, OptimizeLbfgs< Real >::new_x_, OptimizeLbfgs< Real >::num_wolfe_i_failures_, OptimizeLbfgs< Real >::num_wolfe_ii_failures_, OptimizeLbfgs< Real >::opts_, OptimizeLbfgs< Real >::rho_, OptimizeLbfgs< Real >::S(), VectorBase< Real >::SetZero(), kaldi::VecVec(), OptimizeLbfgs< Real >::x_, and OptimizeLbfgs< Real >::Y().

Referenced by OptimizeLbfgs< Real >::DoStep(), OptimizeLbfgs< Real >::Restart(), and OptimizeLbfgs< Real >::StepSizeIteration().

                                                                                {
  KALDI_ASSERT(computation_state_ == kBeforeStep);
  SignedMatrixIndexT m = M(), k = k_;
  ComputeHifNeeded(gradient);
  // The rest of this is computing p_k <-- - H_k \nabla f_k using Algorithm
  // 7.4 of N&W.
  Vector<Real> &q(deriv_), &r(new_x_); // Use deriv_ as a temporary place to put
  // q, and new_x_ as a temporay place to put r.
  // The if-statement below is just to get rid of spurious warnings from
  // valgrind about memcpy source and destination overlap, since sometimes q and
  // gradient are the same variable.
  if (&q != &gradient)
    q.CopyFromVec(gradient); // q <-- \nabla f_k.
  Vector<Real> alpha(m);
  // for i = k - 1, k - 2, ... k - m
  for (SignedMatrixIndexT i = k - 1;
       i >= std::max(k - m, static_cast<SignedMatrixIndexT>(0));
       i--) { 
    alpha(i % m) = rho_(i % m) * VecVec(S(i), q); // \alpha_i <-- \rho_i s_i^T q.
    q.AddVec(-alpha(i % m), Y(i)); // q <-- q - \alpha_i y_i
  }
  r.SetZero();
  r.AddVecVec(1.0, H_, q, 0.0); // r <-- H_k^{(0)} q.
  // for k = k - m, k - m + 1, ... , k - 1
  for (SignedMatrixIndexT i = std::max(k - m, static_cast<SignedMatrixIndexT>(0));
       i < k;
       i++) {
    Real beta = rho_(i % m) * VecVec(Y(i), r); // \beta <-- \rho_i y_i^T r
    r.AddVec(alpha(i % m) - beta, S(i)); // r <-- r + s_i (\alpha_i - \beta)
  }

  { // TEST.  Note, -r will be the direction.
    Real dot = VecVec(gradient, r);
    if ((opts_.minimize && dot < 0) || (!opts_.minimize && dot > 0))
      KALDI_WARN << "Step direction has the wrong sign!  Routine will fail.";
  }
  
  // Now we're out of Alg. 7.4 and back into Alg. 7.5.
  // Alg. 7.4 returned r (using new_x_ as the location), and with \alpha_k = 1
  // as the initial guess, we're setting x_{k+1} = x_k + \alpha_k p_k, with
  // p_k = -r [hence the statement new_x_.Scale(-1.0)]., and \alpha_k = 1.
  // This is the first place we'll get the user to evaluate the function;
  // any backtracking (or acceptance of that step) occurs inside StepSizeIteration.
  // We're still within iteration k; we haven't yet finalized the step size.
  new_x_.Scale(-1.0);
  new_x_.AddVec(1.0, x_);
  if (&deriv_ != &gradient)
    deriv_.CopyFromVec(gradient);
  f_ = function_value;
  d_ = opts_.d;
  num_wolfe_i_failures_ = 0;
  num_wolfe_ii_failures_ = 0;
  last_failure_type_ = kNone;
  computation_state_ = kWithinStep;
}

Dim()

MatrixIndexT Dim ( )

inlineprivate

Definition at line 179 of file optimization.h.

{ return x_.Dim(); }

DoStep() [1/2]

void DoStep	(	Real	function_value,
		const VectorBase< Real > &	gradient
	)

The user calls this function to provide the class with the function and gradient info at the point GetProposedValue().

If this point is outside the constraints you can set function_value to {+infinity,-infinity} for {minimization,maximization} problems. In this case the gradient, and also the second derivative (if you call the second overloaded version of this function) will be ignored.

Definition at line 383 of file optimization.cc.

References OptimizeLbfgs< Real >::best_f_, OptimizeLbfgs< Real >::best_x_, OptimizeLbfgs< Real >::computation_state_, OptimizeLbfgs< Real >::ComputeNewDirection(), OptimizeLbfgs< Real >::kBeforeStep, LbfgsOptions::minimize, OptimizeLbfgs< Real >::new_x_, OptimizeLbfgs< Real >::opts_, and OptimizeLbfgs< Real >::StepSizeIteration().

Referenced by kaldi::nnet2::CombineNnets(), kaldi::nnet2::CombineNnetsA(), LogisticRegression::DoStep(), OptimizeLbfgs< Real >::DoStep(), FastNnetCombiner::FastNnetCombiner(), kaldi::nnet2::ShrinkNnet(), and kaldi::UnitTestLbfgs().

                                                                   {
  if (opts_.minimize ? function_value < best_f_ : function_value > best_f_) {
    best_f_ = function_value;
    best_x_.CopyFromVec(new_x_);
  }
  if (computation_state_ == kBeforeStep)
    ComputeNewDirection(function_value, gradient);
  else // kWithinStep{1,2,3}
    StepSizeIteration(function_value, gradient);
}

DoStep() [2/2]

void DoStep	(	Real	function_value,
		const VectorBase< Real > &	gradient,
		const VectorBase< Real > &	diag_approx_2nd_deriv
	)

The user can call this version of DoStep() if it is desired to set some kind of approximate Hessian on this iteration.

Note: it is a prerequisite that diag_approx_2nd_deriv must be strictly positive (minimizing), or negative (maximizing).

Definition at line 396 of file optimization.cc.

References OptimizeLbfgs< Real >::best_f_, OptimizeLbfgs< Real >::best_x_, OptimizeLbfgs< Real >::DoStep(), OptimizeLbfgs< Real >::H_, OptimizeLbfgs< Real >::H_was_set_, KALDI_ASSERT, VectorBase< Real >::Max(), VectorBase< Real >::Min(), LbfgsOptions::minimize, OptimizeLbfgs< Real >::new_x_, and OptimizeLbfgs< Real >::opts_.

                                                                                {
  if (opts_.minimize ? function_value < best_f_ : function_value > best_f_) {
    best_f_ = function_value;
    best_x_.CopyFromVec(new_x_);
  }
  if (opts_.minimize) {
    KALDI_ASSERT(diag_approx_2nd_deriv.Min() > 0.0);
  } else {
    KALDI_ASSERT(diag_approx_2nd_deriv.Max() < 0.0);
  }
  H_was_set_ = true;
  H_.CopyFromVec(diag_approx_2nd_deriv);
  H_.InvertElements();
  DoStep(function_value, gradient);
}

GetProposedValue()

const VectorBase<Real>& GetProposedValue ( ) const

inline

This returns the value at which the function wants us to compute the objective function and gradient.

Definition at line 134 of file optimization.h.

References KALDI_DISALLOW_COPY_AND_ASSIGN.

Referenced by kaldi::nnet2::CombineNnets(), kaldi::nnet2::CombineNnetsA(), LogisticRegression::DoStep(), FastNnetCombiner::FastNnetCombiner(), kaldi::nnet2::ShrinkNnet(), and kaldi::UnitTestLbfgs().

{ return new_x_; }

GetValue()

const VectorBase< Real > & GetValue

(

Real *

objf_value = NULL

)

const

This returns the value of the variable x that has the best objective function so far, and the corresponding objective function value if requested.

This would typically be called only at the end.

Definition at line 416 of file optimization.cc.

References OptimizeLbfgs< Real >::best_f_, and OptimizeLbfgs< Real >::best_x_.

Referenced by kaldi::nnet2::CombineNnets(), kaldi::nnet2::CombineNnetsA(), FastNnetCombiner::FastNnetCombiner(), kaldi::nnet2::ShrinkNnet(), LogisticRegression::TrainParameters(), and kaldi::UnitTestLbfgs().

                                                    {
  if (objf_value != NULL) *objf_value = best_f_;
  return best_x_;
}

KALDI_DISALLOW_COPY_AND_ASSIGN()

KALDI_DISALLOW_COPY_AND_ASSIGN ( OptimizeLbfgs< Real >  )

private

M()

MatrixIndexT M ( )

inlineprivate

Definition at line 180 of file optimization.h.

Referenced by OptimizeLbfgs< Real >::ComputeNewDirection(), and kaldi::LinearCgd().

{ return opts_.m; }

RecentStepLength()

Real RecentStepLength

(

)

const

Returns the average magnitude of the last n steps (but not more than the number we have stored).

Before we have taken any steps, returns +infinity. Note: if the most recent step length was 0, it returns 0, regardless of the other step lengths. This makes it suitable as a convergence test (else we'd generate NaN's).

Definition at line 55 of file optimization.cc.

References rnnlm::i, rnnlm::n, and OptimizeLbfgs< Real >::step_lengths_.

Referenced by kaldi::UnitTestLbfgs().

                                                 {
  size_t n = step_lengths_.size();
  if (n == 0) return std::numeric_limits<Real>::infinity();
  else {
    if (n >= 2 && step_lengths_[n-1] == 0.0 && step_lengths_[n-2] == 0.0)
      return 0.0; // two zeros in a row means repeated restarts, which is
    // a loop.  Short-circuit this by returning zero.
    Real avg = 0.0;
    for (size_t i = 0; i < n; i++)
      avg += step_lengths_[i] / n;
    return avg;
  }
}

RecordStepLength()

void RecordStepLength ( Real  s )

private

Definition at line 207 of file optimization.cc.

References LbfgsOptions::avg_step_length, OptimizeLbfgs< Real >::opts_, and OptimizeLbfgs< Real >::step_lengths_.

Referenced by OptimizeLbfgs< Real >::AcceptStep(), and OptimizeLbfgs< Real >::Restart().

                                                 {
  step_lengths_.push_back(s);
  if (step_lengths_.size() > static_cast<size_t>(opts_.avg_step_length))
    step_lengths_.erase(step_lengths_.begin(), step_lengths_.begin() + 1);
}

Restart()

void Restart ( const VectorBase< Real > &  x, Real  function_value, const VectorBase< Real > &  gradient  )

private

Definition at line 215 of file optimization.cc.

References VectorBase< Real >::AddVec(), OptimizeLbfgs< Real >::computation_state_, OptimizeLbfgs< Real >::ComputeNewDirection(), VectorBase< Real >::CopyFromVec(), OptimizeLbfgs< Real >::f_, OptimizeLbfgs< Real >::k_, OptimizeLbfgs< Real >::kBeforeStep, OptimizeLbfgs< Real >::new_x_, VectorBase< Real >::Norm(), OptimizeLbfgs< Real >::RecordStepLength(), OptimizeLbfgs< Real >::temp_, and OptimizeLbfgs< Real >::x_.

Referenced by OptimizeLbfgs< Real >::StepSizeIteration().

                                                                    {
  // Note: we will consider restarting (the transition of x_ -> x)
  // as a step, even if it has zero step size.  This is necessary in
  // order for convergence to be detected.
  {
    Vector<Real> &diff(temp_);
    diff.CopyFromVec(x);
    diff.AddVec(-1.0, x_);
    RecordStepLength(diff.Norm(2.0));
  }
  k_ = 0; // Restart the iterations!  [But note that the Hessian,
  // whatever it was, stays as before.]
  if (&x_ != &x)
    x_.CopyFromVec(x);
  new_x_.CopyFromVec(x);
  f_ = f;
  computation_state_ = kBeforeStep;
  ComputeNewDirection(f, gradient);
}

S()

SubVector<Real> S ( MatrixIndexT  i )

inlineprivate

Definition at line 184 of file optimization.h.

References data_.

Referenced by OptimizeLbfgs< Real >::AcceptStep(), OptimizeLbfgs< Real >::ComputeHifNeeded(), and OptimizeLbfgs< Real >::ComputeNewDirection().

                                    {
    return SubVector<Real>(data_, (i % M()) * 2 + 1); // vector s_i
  }

StepSizeIteration()

void StepSizeIteration ( Real  function_value, const VectorBase< Real > &  gradient  )

private

Definition at line 238 of file optimization.cc.

References OptimizeLbfgs< Real >::AcceptStep(), LbfgsOptions::c1, LbfgsOptions::c2, OptimizeLbfgs< Real >::computation_state_, OptimizeLbfgs< Real >::ComputeNewDirection(), OptimizeLbfgs< Real >::d_, OptimizeLbfgs< Real >::deriv_, OptimizeLbfgs< Real >::f_, OptimizeLbfgs< Real >::k_, KALDI_VLOG, OptimizeLbfgs< Real >::kBeforeStep, OptimizeLbfgs< Real >::kWolfeI, OptimizeLbfgs< Real >::kWolfeII, OptimizeLbfgs< Real >::last_failure_type_, LbfgsOptions::max_line_search_iters, LbfgsOptions::minimize, OptimizeLbfgs< Real >::new_x_, OptimizeLbfgs< Real >::num_wolfe_i_failures_, OptimizeLbfgs< Real >::num_wolfe_ii_failures_, OptimizeLbfgs< Real >::opts_, OptimizeLbfgs< Real >::Restart(), OptimizeLbfgs< Real >::temp_, kaldi::VecVec(), and OptimizeLbfgs< Real >::x_.

Referenced by OptimizeLbfgs< Real >::DoStep().

                                                                              {
  KALDI_VLOG(3) << "In step size iteration, function value changed "
                << f_ << " to " << function_value;
  
  // We're in some part of the backtracking, and the user is providing
  // the objective function value and gradient.
  // We're checking two conditions: Wolfe i) [the Armijo rule] and
  // Wolfe ii).
  
  // The Armijo rule (when minimizing) is:
  // f(k_k + \alpha_k p_k) <= f(x_k) + c_1 \alpha_k p_k^T \nabla f(x_k), where
  //  \nabla means the derivative.
  // Below, "temp" is the RHS of this equation, where (\alpha_k p_k) equals
  // (new_x_ - x_); we don't store \alpha or p_k separately, they are implicit
  // as the difference new_x_ - x_.

  // Below, pf is \alpha_k p_k^T \nabla f(x_k).
  Real pf = VecVec(new_x_, deriv_) - VecVec(x_, deriv_);
  Real temp = f_ + opts_.c1 * pf;
  
  bool wolfe_i_ok;
  if (opts_.minimize) wolfe_i_ok = (function_value <= temp);
  else wolfe_i_ok = (function_value >= temp);
  
  // Wolfe condition ii) can be written as:
  //  p_k^T \nabla f(x_k + \alpha_k p_k) >= c_2 p_k^T \nabla f(x_k)
  // p2f equals \alpha_k p_k^T \nabla f(x_k + \alpha_k p_k), where
  // (\alpha_k p_k^T) is (new_x_ - x_).
  // Note that in our version of Wolfe condition (ii) we have an extra
  // factor alpha, which doesn't affect anything.
  Real p2f = VecVec(new_x_, gradient) - VecVec(x_, gradient);
  //eps = (sizeof(Real) == 4 ? 1.0e-05 : 1.0e-10) *
  //(std::abs(p2f) + std::abs(pf));
  bool wolfe_ii_ok;
  if (opts_.minimize) wolfe_ii_ok = (p2f >= opts_.c2 * pf);
  else wolfe_ii_ok = (p2f <= opts_.c2 * pf);

  enum { kDecrease, kNoChange } d_action; // What do do with d_: leave it alone,
  // or take the square root.
  enum { kAccept, kDecreaseStep, kIncreaseStep, kRestart } iteration_action;
  // What we'll do in the overall iteration: accept this value, DecreaseStep
  // (reduce the step size), IncreaseStep (increase the step size), or kRestart
  // (set k back to zero).  Generally when we can't get both conditions to be
  // true with a reasonable period of time, it makes sense to restart, because
  // probably we've almost converged and got into numerical issues; from here
  // we'll just produced NaN's.  Restarting is a safe thing to do and the outer
  // code will quickly detect convergence.

  d_action = kNoChange; // the default.
  
  if (wolfe_i_ok && wolfe_ii_ok) {
    iteration_action = kAccept;
    d_action = kNoChange; // actually doesn't matter, it'll get reset.
  } else if (!wolfe_i_ok) {
    // If wolfe i) [the Armijo rule] failed then we went too far (or are
    // meeting numerical problems).
    if (last_failure_type_ == kWolfeII) { // Last time we failed it was Wolfe ii).
      // When we switch between them we decrease d.
      d_action = kDecrease;
    }
    iteration_action = kDecreaseStep;
    last_failure_type_ = kWolfeI;
    num_wolfe_i_failures_++;
  } else if (!wolfe_ii_ok) {
    // Curvature condition failed -> we did not go far enough.
    if (last_failure_type_ == kWolfeI) // switching between wolfe i and ii failures->
      d_action = kDecrease; // decrease value of d.
    iteration_action = kIncreaseStep;
    last_failure_type_ = kWolfeII;
    num_wolfe_ii_failures_++;
  }

  // Test whether we've been switching too many times betwen wolfe i) and ii)
  // failures, or overall have an excessive number of failures.  We just give up
  // and restart L-BFGS.  Probably we've almost converged.
  if (num_wolfe_i_failures_ + num_wolfe_ii_failures_ >
      opts_.max_line_search_iters) {
    KALDI_VLOG(2) << "Too many steps in line search -> restarting.";
    iteration_action = kRestart;
  }

  if (d_action == kDecrease)
    d_ = std::sqrt(d_);
  
  KALDI_VLOG(3) << "d = " << d_ << ", iter = " << k_ << ", action = "
                << (iteration_action == kAccept ? "accept" :
                    (iteration_action == kDecreaseStep ? "decrease" :
                     (iteration_action == kIncreaseStep ? "increase" :
                      "reject")));
  
  // Note: even if iteration_action != Restart at this point,
  // some code below may set it to Restart.
  if (iteration_action == kAccept) {
    if (AcceptStep(function_value, gradient)) { // If we did
      // not detect a problem while accepting the step..
      computation_state_ = kBeforeStep;
      ComputeNewDirection(function_value, gradient);
    } else {
      KALDI_VLOG(2) << "Restarting L-BFGS computation; problem found while "
                    << "accepting step.";
      iteration_action = kRestart; // We'll have to restart now.
    }
  }
  if (iteration_action == kDecreaseStep || iteration_action == kIncreaseStep) {
    Real scale = (iteration_action == kDecreaseStep ? 1.0 / d_ : d_);
    temp_.CopyFromVec(new_x_);
    new_x_.Scale(scale);
    new_x_.AddVec(1.0 - scale, x_);
    if (new_x_.ApproxEqual(temp_, 0.0)) {
      // Value of new_x_ did not change at all --> we must restart.
      KALDI_VLOG(3) << "Value of x did not change, when taking step; "
                    << "will restart computation.";
      iteration_action = kRestart;
    }
    if (new_x_.ApproxEqual(temp_, 1.0e-08) &&
        std::abs(f_ - function_value) < 1.0e-08 *
        std::abs(f_) && iteration_action == kDecreaseStep) {
      // This is common and due to roundoff.
      KALDI_VLOG(3) << "We appear to be backtracking while we are extremely "
                    << "close to the old value; restarting.";
      iteration_action = kRestart;
    }
        
    if (iteration_action == kDecreaseStep) {
      num_wolfe_i_failures_++;
      last_failure_type_ = kWolfeI;
    } else {
      num_wolfe_ii_failures_++;
      last_failure_type_ = kWolfeII;
    }
  }
  if (iteration_action == kRestart) {
    // We want to restart the computation.  If the objf at new_x_ is
    // better than it was at x_, we'll start at new_x_, else at x_.
    bool use_newx;
    if (opts_.minimize) use_newx = (function_value < f_);
    else use_newx = (function_value > f_);
    KALDI_VLOG(3) << "Restarting computation.";
    if (use_newx) Restart(new_x_, function_value, gradient);
    else Restart(x_, f_, deriv_);
  }
}

Y()

SubVector<Real> Y ( MatrixIndexT  i )

inlineprivate

Definition at line 181 of file optimization.h.

References data_.

Referenced by OptimizeLbfgs< Real >::AcceptStep(), OptimizeLbfgs< Real >::ComputeHifNeeded(), and OptimizeLbfgs< Real >::ComputeNewDirection().

                                    {
    return SubVector<Real>(data_, (i % M()) * 2); // vector y_i
  }

Member Data Documentation

best_f_

Real best_f_

private

Definition at line 217 of file optimization.h.

Referenced by OptimizeLbfgs< Real >::DoStep(), OptimizeLbfgs< Real >::GetValue(), and OptimizeLbfgs< Real >::OptimizeLbfgs().

best_x_

Vector<Real> best_x_

private

Definition at line 212 of file optimization.h.

Referenced by OptimizeLbfgs< Real >::DoStep(), OptimizeLbfgs< Real >::GetValue(), and OptimizeLbfgs< Real >::OptimizeLbfgs().

computation_state_

ComputationState computation_state_

private

Definition at line 205 of file optimization.h.

Referenced by OptimizeLbfgs< Real >::ComputeNewDirection(), OptimizeLbfgs< Real >::DoStep(), OptimizeLbfgs< Real >::Restart(), and OptimizeLbfgs< Real >::StepSizeIteration().

d_

Real d_

private

Definition at line 218 of file optimization.h.

Referenced by OptimizeLbfgs< Real >::ComputeNewDirection(), and OptimizeLbfgs< Real >::StepSizeIteration().

data_

Matrix<Real> data_

private

Definition at line 228 of file optimization.h.

Referenced by OptimizeLbfgs< Real >::OptimizeLbfgs().

deriv_

Vector<Real> deriv_

private

Definition at line 214 of file optimization.h.

Referenced by OptimizeLbfgs< Real >::AcceptStep(), OptimizeLbfgs< Real >::ComputeNewDirection(), OptimizeLbfgs< Real >::OptimizeLbfgs(), and OptimizeLbfgs< Real >::StepSizeIteration().

f_

Real f_

private

Definition at line 216 of file optimization.h.

Referenced by OptimizeLbfgs< Real >::AcceptStep(), OptimizeLbfgs< Real >::ComputeNewDirection(), OptimizeLbfgs< Real >::OptimizeLbfgs(), OptimizeLbfgs< Real >::Restart(), and OptimizeLbfgs< Real >::StepSizeIteration().

H_

Vector<Real> H_

private

Definition at line 226 of file optimization.h.

Referenced by OptimizeLbfgs< Real >::ComputeHifNeeded(), OptimizeLbfgs< Real >::ComputeNewDirection(), and OptimizeLbfgs< Real >::DoStep().

H_was_set_

bool H_was_set_

private

Definition at line 206 of file optimization.h.

Referenced by OptimizeLbfgs< Real >::ComputeHifNeeded(), and OptimizeLbfgs< Real >::DoStep().

k_

SignedMatrixIndexT k_

private

Definition at line 202 of file optimization.h.

Referenced by OptimizeLbfgs< Real >::AcceptStep(), OptimizeLbfgs< Real >::ComputeHifNeeded(), OptimizeLbfgs< Real >::ComputeNewDirection(), OptimizeLbfgs< Real >::Restart(), and OptimizeLbfgs< Real >::StepSizeIteration().

last_failure_type_

enum { ... } last_failure_type_

Referenced by OptimizeLbfgs< Real >::ComputeNewDirection(), and OptimizeLbfgs< Real >::StepSizeIteration().

new_x_

Vector<Real> new_x_

private

Definition at line 211 of file optimization.h.

Referenced by OptimizeLbfgs< Real >::AcceptStep(), OptimizeLbfgs< Real >::ComputeNewDirection(), OptimizeLbfgs< Real >::DoStep(), OptimizeLbfgs< Real >::OptimizeLbfgs(), OptimizeLbfgs< Real >::Restart(), and OptimizeLbfgs< Real >::StepSizeIteration().

num_wolfe_i_failures_

int num_wolfe_i_failures_

private

Definition at line 221 of file optimization.h.

Referenced by OptimizeLbfgs< Real >::ComputeNewDirection(), and OptimizeLbfgs< Real >::StepSizeIteration().

num_wolfe_ii_failures_

int num_wolfe_ii_failures_

private

Definition at line 222 of file optimization.h.

Referenced by OptimizeLbfgs< Real >::ComputeNewDirection(), and OptimizeLbfgs< Real >::StepSizeIteration().

opts_

LbfgsOptions opts_

private

Definition at line 201 of file optimization.h.

Referenced by OptimizeLbfgs< Real >::AcceptStep(), OptimizeLbfgs< Real >::ComputeHifNeeded(), OptimizeLbfgs< Real >::ComputeNewDirection(), OptimizeLbfgs< Real >::DoStep(), OptimizeLbfgs< Real >::RecordStepLength(), and OptimizeLbfgs< Real >::StepSizeIteration().

rho_

Vector<Real> rho_

private

Definition at line 230 of file optimization.h.

Referenced by OptimizeLbfgs< Real >::AcceptStep(), OptimizeLbfgs< Real >::ComputeNewDirection(), and OptimizeLbfgs< Real >::OptimizeLbfgs().

step_lengths_

std::vector<Real> step_lengths_

private

Definition at line 232 of file optimization.h.

Referenced by OptimizeLbfgs< Real >::RecentStepLength(), and OptimizeLbfgs< Real >::RecordStepLength().

temp_

Vector<Real> temp_

private

Definition at line 215 of file optimization.h.

Referenced by OptimizeLbfgs< Real >::OptimizeLbfgs(), OptimizeLbfgs< Real >::Restart(), and OptimizeLbfgs< Real >::StepSizeIteration().

x_

Vector<Real> x_

private

Definition at line 210 of file optimization.h.

Referenced by OptimizeLbfgs< Real >::AcceptStep(), OptimizeLbfgs< Real >::ComputeHifNeeded(), OptimizeLbfgs< Real >::ComputeNewDirection(), OptimizeLbfgs< Real >::OptimizeLbfgs(), OptimizeLbfgs< Real >::Restart(), and OptimizeLbfgs< Real >::StepSizeIteration().

---

The documentation for this class was generated from the following files:

• matrix/optimization.h
• matrix/optimization.cc