Collaboration diagram for Miscellaneous matrix/vector library functions and classes:

Classes
struct	SolverOptions
	This class describes the options for maximizing various quadratic objective functions. More...

class	SplitRadixComplexFft< Real >

class	SplitRadixRealFft< Real >

Functions
template<typename Real >
void	SortSvd (VectorBase< Real > s, MatrixBase< Real > U, MatrixBase< Real > *Vt=NULL, bool sort_on_absolute_value=true)
	Function to ensure that SVD is sorted. More...

template<typename Real >
void	CreateEigenvalueMatrix (const VectorBase< Real > &real, const VectorBase< Real > &imag, MatrixBase< Real > *D)
	Creates the eigenvalue matrix D that is part of the decomposition used Matrix::Eig. More...

template<typename Real >
bool	AttemptComplexPower (Real x_re, Real x_im, Real power)
	The following function is used in Matrix::Power, and separately tested, so we declare it here mainly for the testing code to see. More...

template<typename Real >
void	ComplexFft (VectorBase< Real > v, bool forward, Vector< Real > tmp_work=NULL)
	The function ComplexFft does an Fft on the vector argument v. More...

template<typename Real >
void	ComplexFt (const VectorBase< Real > &in, VectorBase< Real > *out, bool forward)
	ComplexFt is the same as ComplexFft but it implements the Fourier transform in an inefficient way. More...

template<typename Real >
void	RealFft (VectorBase< Real > *v, bool forward)
	RealFft is a fourier transform of real inputs. More...

template<typename Real >
void	RealFftInefficient (VectorBase< Real > *v, bool forward)
	Inefficient version of Fourier transform, for testing purposes. More...

template<typename Real >
void	ComputeDctMatrix (Matrix< Real > *M)
	ComputeDctMatrix computes a matrix corresponding to the DCT, such that M * v equals the DCT of vector v. More...

template<typename Real >
void	ComplexMul (const Real &a_re, const Real &a_im, Real b_re, Real b_im)
	ComplexMul implements, inline, the complex multiplication b *= a. More...

template<typename Real >
void	ComplexAddProduct (const Real &a_re, const Real &a_im, const Real &b_re, const Real &b_im, Real c_re, Real c_im)
	ComplexMul implements, inline, the complex operation c += (a * b). More...

template<typename Real >
void	ComplexImExp (Real x, Real a_re, Real a_im)
	ComplexImExp implements a <– exp(i x), inline. More...

template<typename Real >
void	ComputePca (const MatrixBase< Real > &X, MatrixBase< Real > U, MatrixBase< Real > A, bool print_eigs=false, bool exact=true)
	ComputePCA does a PCA computation, using either outer products or inner products, whichever is more efficient. More...

template<typename Real >
void	AddOuterProductPlusMinus (Real alpha, const VectorBase< Real > &a, const VectorBase< Real > &b, MatrixBase< Real > plus, MatrixBase< Real > minus)

template<typename Real1 , typename Real2 >
void	AssertSameDim (const MatrixBase< Real1 > &mat1, const MatrixBase< Real2 > &mat2)

template<typename Real >
Real	SolveQuadraticProblem (const SpMatrix< Real > &H, const VectorBase< Real > &g, const SolverOptions &opts, VectorBase< Real > *x)
	Maximizes the auxiliary function $Q(x) = x.g - 0.5 x^T H x$ using a numerically stable method. More...

template<typename Real >
Real	SolveQuadraticMatrixProblem (const SpMatrix< Real > &Q, const MatrixBase< Real > &Y, const SpMatrix< Real > &P, const SolverOptions &opts, MatrixBase< Real > *M)
	Maximizes the auxiliary function : $Q(x) = tr(M^T P Y) - 0.5 tr(P M Q M^T)$ Like a numerically stable version of $M := Y Q^{-1}$ . More...

template<typename Real >
Real	SolveDoubleQuadraticMatrixProblem (const MatrixBase< Real > &G, const SpMatrix< Real > &P1, const SpMatrix< Real > &P2, const SpMatrix< Real > &Q1, const SpMatrix< Real > &Q2, const SolverOptions &opts, MatrixBase< Real > *M)
	Maximizes the auxiliary function : $Q(M) = tr(M^T G) -0.5 tr(P_1 M Q_1 M^T) -0.5 tr(P_2 M Q_2 M^T).$ Encountered in matrix update with a prior. More...

Detailed Description

Function Documentation

◆ AddOuterProductPlusMinus()

void AddOuterProductPlusMinus	(	Real	alpha,
		const VectorBase< Real > &	a,
		const VectorBase< Real > &	b,
		MatrixBase< Real > *	plus,
		MatrixBase< Real > *	minus
	)

Definition at line 726 of file matrix-functions.cc.

References kaldi::AddOuterProductPlusMinus< double >(), kaldi::AddOuterProductPlusMinus< float >(), VectorBase< Real >::Data(), MatrixBase< Real >::Data(), VectorBase< Real >::Dim(), rnnlm::i, rnnlm::j, KALDI_ASSERT, MatrixBase< Real >::NumCols(), MatrixBase< Real >::NumRows(), and MatrixBase< Real >::Stride().

Referenced by Fmpe::ApplyProjectionReverse(), and kaldi::UnitTestAddOuterProductPlusMinus().

                                                        {
   KALDI_ASSERT(a.Dim() == plus->NumRows() && b.Dim() == plus->NumCols()
                && a.Dim() == minus->NumRows() && b.Dim() == minus->NumCols());
   int32 nrows = a.Dim(), ncols = b.Dim(), pskip = plus->Stride() - ncols,
       mskip = minus->Stride() - ncols;
   const Real *adata = a.Data(), *bdata = b.Data();
   Real *plusdata = plus->Data(), *minusdata = minus->Data();
 
   for (int32 i = 0; i < nrows; i++) {
     const Real *btmp = bdata;
     Real multiple = alpha * *adata;
     if (multiple > 0.0) {
       for (int32 j = 0; j < ncols; j++, plusdata++, minusdata++, btmp++) {
         if (*btmp > 0.0) *plusdata += multiple * *btmp;
         else *minusdata -= multiple * *btmp;
       }
     } else {
       for (int32 j = 0; j < ncols; j++, plusdata++, minusdata++, btmp++) {
         if (*btmp < 0.0) *plusdata += multiple * *btmp;
         else *minusdata -= multiple * *btmp;
       }
     }
     plusdata += pskip;
     minusdata += mskip;
     adata++;
   }
 }

◆ AssertSameDim()

void kaldi::AssertSameDim	(	const MatrixBase< Real1 > &	mat1,
		const MatrixBase< Real2 > &	mat2
	)

inline

Definition at line 161 of file matrix-functions.h.

References KALDI_ASSERT, MatrixBase< Real >::NumCols(), and MatrixBase< Real >::NumRows().

                                                                                         {
   KALDI_ASSERT(mat1.NumRows() == mat2.NumRows()
                && mat1.NumCols() == mat2.NumCols());
 }

◆ AttemptComplexPower()

bool AttemptComplexPower	(	Real *	x_re,
		Real *	x_im,
		Real	power
	)

The following function is used in Matrix::Power, and separately tested, so we declare it here mainly for the testing code to see.

It takes a complex value to a power using a method that will work for noninteger powers (but will fail if the complex value is real and negative).

Definition at line 2659 of file kaldi-matrix.cc.

References kaldi::AttemptComplexPower().

Referenced by kaldi::TraceMat(), and kaldi::UnitTestComplexPower().

                                                              {
   // Used in Matrix<Real>::Power().
   // Attempts to take the complex value x to the power "power",
   // assuming that power is fractional (i.e. we don't treat integers as a
   // special case).  Returns false if this is not possible, either
   // because x is negative and real (hence there is no obvious answer
   // that is "closest to 1", and anyway this case does not make sense
   // in the Matrix<Real>::Power() routine);
   // or because power is negative, and x is zero.
 
   // First solve for r and theta in
   // x_re = r*cos(theta), x_im = r*sin(theta)
   if (*x_re < 0.0 && *x_im == 0.0) return false;  // can't do
   // it for negative real values.
   Real r = std::sqrt((*x_re * *x_re) + (*x_im * *x_im));  // r == radius.
   if (power < 0.0 && r == 0.0) return false;
   Real theta = std::atan2(*x_im, *x_re);
   // Take the power.
   r = std::pow(r, power);
   theta *= power;
   *x_re = r * std::cos(theta);
   *x_im = r * std::sin(theta);
   return true;
 }

◆ ComplexAddProduct()

void ComplexAddProduct	(	const Real &	a_re,
		const Real &	a_im,
		const Real &	b_re,
		const Real &	b_im,
		Real *	c_re,
		Real *	c_im
	)

inline

ComplexMul implements, inline, the complex operation c += (a * b).

Definition at line 38 of file matrix-functions-inl.h.

Referenced by kaldi::ComplexFftRecursive(), kaldi::ComplexFt(), SplitRadixRealFft< float >::Compute(), and kaldi::RealFft().

                                                                            {
   *c_re += b_re*a_re - b_im*a_im;
   *c_im += b_re*a_im + b_im*a_re;
 }

◆ ComplexFft()

void ComplexFft	(	VectorBase< Real > *	v,
		bool	forward,
		Vector< Real > *	tmp_work = `NULL`
	)

The function ComplexFft does an Fft on the vector argument v.

v is a vector of even dimension, interpreted for both input and output as a vector of complex numbers i.e.

$v = ( re_0, im_0, re_1, im_1, ... )$

If "forward == true" this routine does the Discrete Fourier Transform (DFT), i.e.:

$vout[m] \leftarrow \sum_{n = 0}^{N-1} vin[i] exp( -2pi m n / N )$

If "backward" it does the Inverse Discrete Fourier Transform (IDFT) WITHOUT THE FACTOR 1/N*, i.e.:

$vout[m] <-- \sum_{n = 0}^{N-1} vin[i] exp( 2pi m n / N )$

[note the sign difference on the 2 pi for the backward one.]

Note that this is the definition of the FT given in most texts, but it differs from the Numerical Recipes version in which the forward and backward algorithms are flipped.

Note that you would have to multiply by 1/N after the IDFT to get back to where you started from. We don't do this because in some contexts, the transform is made symmetric by multiplying by sqrt(N) in both passes. The user can do this by themselves.

See also SplitRadixComplexFft, declared in srfft.h, which is more efficient but only works if the length of the input is a power of 2.

Definition at line 334 of file matrix-functions.cc.

References kaldi::ComplexFftRecursive(), VectorBase< Real >::Data(), VectorBase< Real >::Dim(), kaldi::Factorize(), and KALDI_ASSERT.

Referenced by kaldi::RealFft(), kaldi::RealFftInefficient(), kaldi::UnitTestComplexFft(), and kaldi::UnitTestComplexFft2().

                                                                                                  {
   KALDI_ASSERT(v != NULL);
 
   if (v->Dim()<=1) return;
   KALDI_ASSERT(v->Dim() % 2 == 0);  // complex input.
   int N = v->Dim() / 2;
   std::vector<int> factors;
   Factorize(N, &factors);
   int *factor_beg = NULL;
   if (factors.size() > 0)
     factor_beg = &(factors[0]);
   Vector<Real> tmp;  // allocated in ComplexFftRecursive.
   ComplexFftRecursive(v->Data(), 1, N, factor_beg, factor_beg+factors.size(), forward, (tmp_in?tmp_in:&tmp));
 }

◆ ComplexFt()

void ComplexFt	(	const VectorBase< Real > &	in,
		VectorBase< Real > *	out,
		bool	forward
	)

ComplexFt is the same as ComplexFft but it implements the Fourier transform in an inefficient way.

It is mainly included for testing purposes. See comment for ComplexFft to describe the input and outputs and what it does.

Definition at line 29 of file matrix-functions.cc.

References kaldi::ComplexAddProduct(), kaldi::ComplexImExp(), kaldi::ComplexMul(), VectorBase< Real >::Data(), VectorBase< Real >::Dim(), KALDI_ASSERT, and M_2PI.

Referenced by kaldi::UnitTestComplexFft(), kaldi::UnitTestComplexFft2(), kaldi::UnitTestComplexFt(), and kaldi::UnitTestSplitRadixComplexFft().

                                                                           {
   int exp_sign = (forward ? -1 : 1);
   KALDI_ASSERT(out != NULL);
   KALDI_ASSERT(in.Dim() == out->Dim());
   KALDI_ASSERT(in.Dim() % 2 == 0);
   int twoN = in.Dim(), N = twoN / 2;
   const Real *data_in = in.Data();
   Real *data_out = out->Data();
 
   Real exp1N_re, exp1N_im;  //  forward -> exp(-2pi / N), backward -> exp(2pi / N).
   Real fraction = exp_sign * M_2PI / static_cast<Real>(N);  // forward -> -2pi/N, backward->-2pi/N
   ComplexImExp(fraction, &exp1N_re, &exp1N_im);
 
   Real expm_re = 1.0, expm_im = 0.0;  // forward -> exp(-2pi m / N).
 
   for (int two_m = 0; two_m < twoN; two_m+=2) {  // For each output component.
     Real expmn_re = 1.0, expmn_im = 0.0;  // forward -> exp(-2pi m n / N).
     Real sum_re = 0.0, sum_im = 0.0;  // complex output for index m (the sum expression)
     for (int two_n = 0; two_n < twoN; two_n+=2) {
       ComplexAddProduct(data_in[two_n], data_in[two_n+1],
                         expmn_re, expmn_im,
                         &sum_re, &sum_im);
       ComplexMul(expm_re, expm_im, &expmn_re, &expmn_im);
     }
     data_out[two_m] = sum_re;
     data_out[two_m + 1] = sum_im;
 
 
     if (two_m % 10 == 0) {  // occasionally renew "expm" from scratch to avoid
       // loss of precision.
       int nextm = 1 + two_m/2;
       Real fraction_mult = fraction * nextm;
       ComplexImExp(fraction_mult, &expm_re, &expm_im);
     } else {
       ComplexMul(exp1N_re, exp1N_im, &expm_re, &expm_im);
     }
   }
 }

◆ ComplexImExp()

void ComplexImExp	(	Real	x,
		Real *	a_re,
		Real *	a_im
	)

inline

ComplexImExp implements a <– exp(i x), inline.

Definition at line 46 of file matrix-functions-inl.h.

Referenced by kaldi::ComplexFftRecursive(), kaldi::ComplexFt(), SplitRadixRealFft< float >::Compute(), and kaldi::RealFft().

                                                                                  {
   *a_re = std::cos(x);
   *a_im = std::sin(x);
 }

◆ ComplexMul()

void ComplexMul	(	const Real &	a_re,
		const Real &	a_im,
		Real *	b_re,
		Real *	b_im
	)

inline

ComplexMul implements, inline, the complex multiplication b *= a.

Definition at line 31 of file matrix-functions-inl.h.

Referenced by kaldi::ComplexFftRecursive(), kaldi::ComplexFt(), SplitRadixRealFft< float >::Compute(), kaldi::ElementwiseProductOfFft(), and kaldi::RealFft().

                                                                     {
   Real tmp_re = (*b_re * a_re) - (*b_im * a_im);
   *b_im = *b_re * a_im + *b_im * a_re;
   *b_re = tmp_re;
 }

◆ ComputeDctMatrix()

void ComputeDctMatrix ( Matrix< Real > * M )

ComputeDctMatrix computes a matrix corresponding to the DCT, such that M * v equals the DCT of vector v.

M must be square at input. This is the type = III DCT with normalization, corresponding to the following equations, where x is the signal and X is the DCT: X_0 = 1/sqrt(2*N) {n = 0}^{N-1} x_n X_k = 1/sqrt(N) {n = 0}^{N-1} x_n cos( /N (n + 1/2) k ) This matrix's transpose is its own inverse, so transposing this matrix will give the inverse DCT. Caution: the type III DCT is generally known as the "inverse DCT" (with the type II being the actual DCT), so this function is somewhatd mis-named. It was probably done this way for HTK compatibility. We don't change it because it was this way from the start and changing it would affect the feature generation.

Definition at line 592 of file matrix-functions.cc.

References rnnlm::j, KALDI_ASSERT, M_PI, rnnlm::n, MatrixBase< Real >::NumCols(), and MatrixBase< Real >::NumRows().

Referenced by DctComponent::Init(), MfccComputer::MfccComputer(), and kaldi::UnitTestDct().

                                                                {
   //KALDI_ASSERT(M->NumRows() == M->NumCols());
   MatrixIndexT K = M->NumRows();
   MatrixIndexT N = M->NumCols();
 
   KALDI_ASSERT(K > 0);
   KALDI_ASSERT(N > 0);
   Real normalizer = std::sqrt(1.0 / static_cast<Real>(N));  // normalizer for
   // X_0.
   for (MatrixIndexT j = 0; j < N; j++) (*M)(0, j) = normalizer;
   normalizer = std::sqrt(2.0 / static_cast<Real>(N));  // normalizer for other
    // elements.
   for (MatrixIndexT k = 1; k < K; k++)
     for (MatrixIndexT n = 0; n < N; n++)
       (*M)(k, n) = normalizer
           * std::cos( static_cast<double>(M_PI)/N * (n + 0.5) * k );
 }

◆ ComputePca()

void ComputePca	(	const MatrixBase< Real > &	X,
		MatrixBase< Real > *	U,
		MatrixBase< Real > *	A,
		bool	print_eigs = `false`,
		bool	exact = `true`
	)

ComputePCA does a PCA computation, using either outer products or inner products, whichever is more efficient.

Let D be the dimension of the data points, N be the number of data points, and G be the PCA dimension we want to retain. We assume G <= N and G <= D.

Parameters

X	[in] An N x D matrix. Each row of X is a point x_i.
U	[out] A G x D matrix. Each row of U is a basis element u_i.
A	[out] An N x D matrix, or NULL. Each row of A is a set of coefficients in the basis for a point x_i, so A(i, g) is the coefficient of u_i in x_i.
print_eigs	[in] If true, prints out diagnostic information about the eigenvalues.
exact	[in] If true, does the exact computation; if false, does a much faster (but almost exact) computation based on the Lanczos method.

Definition at line 616 of file matrix-functions.cc.

References SpMatrix< Real >::AddMat2(), MatrixBase< Real >::AddMatMat(), MatrixBase< Real >::DestructiveSvd(), SpMatrix< Real >::Eig(), KALDI_ASSERT, KALDI_LOG, KALDI_WARN, kaldi::kNoTrans, kaldi::kTrans, rnnlm::n, MatrixBase< Real >::NumCols(), MatrixBase< Real >::NumRows(), MatrixBase< Real >::OrthogonalizeRows(), Vector< Real >::Resize(), Matrix< Real >::Resize(), MatrixBase< Real >::Row(), kaldi::SortSvd(), SpMatrix< Real >::TopEigs(), and Matrix< Real >::Transpose().

Referenced by kaldi::UnitTestPca(), and kaldi::UnitTestPca2().

                             {
   // Note that some of these matrices may be transposed w.r.t. the
   // way it's most natural to describe them in math... it's the rows
   // of X and U that correspond to the (data-points, basis elements).
   MatrixIndexT N = X.NumRows(), D = X.NumCols();
   // N = #points, D = feature dim.
   KALDI_ASSERT(U != NULL && U->NumCols() == D);
   MatrixIndexT G = U->NumRows();  // # of retained basis elements.
   KALDI_ASSERT(A == NULL || (A->NumRows() == N && A->NumCols() == G));
   KALDI_ASSERT(G <= N && G <= D);
   if (D < N) {  // Do conventional PCA.
     SpMatrix<Real> Msp(D);  // Matrix of outer products.
     Msp.AddMat2(1.0, X, kTrans, 0.0);  // M <-- X^T X
     Matrix<Real> Utmp;
     Vector<Real> l;
     if (exact) {
       Utmp.Resize(D, D);
       l.Resize(D);
       //Matrix<Real> M(Msp);
       //M.DestructiveSvd(&l, &Utmp, NULL);
       Msp.Eig(&l, &Utmp);
     } else {
       Utmp.Resize(D, G);
       l.Resize(G);
       Msp.TopEigs(&l, &Utmp);
     }
     SortSvd(&l, &Utmp);
 
     for (MatrixIndexT g = 0; g < G; g++)
       U->Row(g).CopyColFromMat(Utmp, g);
     if (print_eigs)
       KALDI_LOG << (exact ? "" : "Retained ")
                 << "PCA eigenvalues are " << l;
     if (A != NULL)
       A->AddMatMat(1.0, X, kNoTrans, *U, kTrans, 0.0);
   } else {  // Do inner-product PCA.
     SpMatrix<Real> Nsp(N);  // Matrix of inner products.
     Nsp.AddMat2(1.0, X, kNoTrans, 0.0);  // M <-- X X^T
 
     Matrix<Real> Vtmp;
     Vector<Real> l;
     if (exact) {
       Vtmp.Resize(N, N);
       l.Resize(N);
       Matrix<Real> Nmat(Nsp);
       Nmat.DestructiveSvd(&l, &Vtmp, NULL);
     } else {
       Vtmp.Resize(N, G);
       l.Resize(G);
       Nsp.TopEigs(&l, &Vtmp);
     }
 
     MatrixIndexT num_zeroed = 0;
     for (MatrixIndexT g = 0; g < G; g++) {
       if (l(g) < 0.0) {
         KALDI_WARN << "In PCA, setting element " << l(g) << " to zero.";
         l(g) = 0.0;
         num_zeroed++;
       }
     }
     SortSvd(&l, &Vtmp); // Make sure zero elements are last, this
     // is necessary for Orthogonalize() to work properly later.
 
     Vtmp.Transpose();  // So eigenvalues are the rows.
 
     for (MatrixIndexT g = 0; g < G; g++) {
       Real sqrtlg = sqrt(l(g));
       if (l(g) != 0.0) {
         U->Row(g).AddMatVec(1.0 / sqrtlg, X, kTrans, Vtmp.Row(g), 0.0);
       } else {
         U->Row(g).SetZero();
         (*U)(g, g) = 1.0;  // arbitrary direction.  Will later orthogonalize.
       }
       if (A != NULL)
         for (MatrixIndexT n = 0; n < N; n++)
           (*A)(n, g) = sqrtlg * Vtmp(g, n);
     }
     // Now orthogonalize.  This is mainly useful in
     // case there were zero eigenvalues, but we do it
     // for all of them.
     U->OrthogonalizeRows();
     if (print_eigs)
       KALDI_LOG << "(inner-product) PCA eigenvalues are " << l;
   }
 }

◆ CreateEigenvalueMatrix()

void CreateEigenvalueMatrix	(	const VectorBase< Real > &	real,
		const VectorBase< Real > &	imag,
		MatrixBase< Real > *	D
	)

Creates the eigenvalue matrix D that is part of the decomposition used Matrix::Eig.

D will be block-diagonal with blocks of size 1 (for real eigenvalues) or 2x2 for complex pairs. If a complex pair is lambda +- i*mu, D will have a corresponding 2x2 block [lambda, mu; -mu, lambda]. This function will throw if any complex eigenvalues are not in complex conjugate pairs (or the members of such pairs are not consecutively numbered).

if (im(j) < 0.0) KALDI_WARN << "Negative first im part of pair"; // TEMP

Definition at line 2623 of file kaldi-matrix.cc.

References kaldi::ApproxEqual(), kaldi::CreateEigenvalueMatrix(), VectorBase< Real >::Dim(), rnnlm::j, KALDI_ASSERT, rnnlm::n, MatrixBase< Real >::NumCols(), MatrixBase< Real >::NumRows(), and MatrixBase< Real >::SetZero().

Referenced by kaldi::TraceMat(), and kaldi::UnitTestEig().

                                                  {
   MatrixIndexT n = re.Dim();
   KALDI_ASSERT(im.Dim() == n && D->NumRows() == n && D->NumCols() == n);
 
   MatrixIndexT j = 0;
   D->SetZero();
   while (j < n) {
     if (im(j) == 0) {  // Real eigenvalue
       (*D)(j, j) = re(j);
       j++;
     } else {  // First of a complex pair
       KALDI_ASSERT(j+1 < n && ApproxEqual(im(j+1), -im(j))
                    && ApproxEqual(re(j+1), re(j)));
       Real lambda = re(j), mu = im(j);
       // create 2x2 block [lambda, mu; -mu, lambda]
       (*D)(j, j) = lambda;
       (*D)(j, j+1) = mu;
       (*D)(j+1, j) = -mu;
       (*D)(j+1, j+1) = lambda;
       j += 2;
     }
   }
 }

◆ RealFft()

void RealFft	(	VectorBase< Real > *	v,
		bool	forward
	)

RealFft is a fourier transform of real inputs.

Internally it uses ComplexFft. The input dimension N must be even. If forward == true, it transforms from a sequence of N real points to its complex fourier transform; otherwise it goes in the reverse direction. If you call it in the forward and then reverse direction and multiply by 1.0/N, you will get back the original data. The interpretation of the complex-FFT data is as follows: the array is a sequence of complex numbers C_n of length N/2 with (real, im) format, i.e. [real0, real_{N/2}, real1, im1, real2, im2, real3, im3, ...]. See also SplitRadixRealFft, declared in srfft.h, which is more efficient but only works if the length of the input is a power of 2.

Definition at line 391 of file matrix-functions.cc.

References kaldi::ComplexAddProduct(), kaldi::ComplexFft(), kaldi::ComplexImExp(), kaldi::ComplexMul(), VectorBase< Real >::Data(), VectorBase< Real >::Dim(), KALDI_ASSERT, M_2PI, and VectorBase< Real >::Scale().

Referenced by SpectrogramComputer::Compute(), MfccComputer::Compute(), FbankComputer::Compute(), PlpComputer::Compute(), kaldi::UnitTestRealFft(), and kaldi::UnitTestRealFftSpeed().

                                                                          {
   KALDI_ASSERT(v != NULL);
   MatrixIndexT N = v->Dim(), N2 = N/2;
   KALDI_ASSERT(N%2 == 0);
   if (N == 0) return;
 
   if (forward) ComplexFft(v, true);
 
   Real *data = v->Data();
   Real rootN_re, rootN_im;  // exp(-2pi/N), forward; exp(2pi/N), backward
   int forward_sign = forward ? -1 : 1;
   ComplexImExp(static_cast<Real>(M_2PI/N *forward_sign), &rootN_re, &rootN_im);
   Real kN_re = -forward_sign, kN_im = 0.0;  // exp(-2pik/N), forward; exp(-2pik/N), backward
   // kN starts out as 1.0 for forward algorithm but -1.0 for backward.
   for (MatrixIndexT k = 1; 2*k <= N2; k++) {
     ComplexMul(rootN_re, rootN_im, &kN_re, &kN_im);
 
     Real Ck_re, Ck_im, Dk_re, Dk_im;
     // C_k = 1/2 (B_k + B_{N/2 - k}^*) :
     Ck_re = 0.5 * (data[2*k] + data[N - 2*k]);
     Ck_im = 0.5 * (data[2*k + 1] - data[N - 2*k + 1]);
     // re(D_k)= 1/2 (im(B_k) + im(B_{N/2-k})):
     Dk_re = 0.5 * (data[2*k + 1] + data[N - 2*k + 1]);
     // im(D_k) = -1/2 (re(B_k) - re(B_{N/2-k}))
     Dk_im =-0.5 * (data[2*k] - data[N - 2*k]);
     // A_k = C_k + 1^(k/N) D_k:
     data[2*k] = Ck_re;  // A_k <-- C_k
     data[2*k+1] = Ck_im;
     // now A_k += D_k 1^(k/N)
     ComplexAddProduct(Dk_re, Dk_im, kN_re, kN_im, &(data[2*k]), &(data[2*k+1]));
 
     MatrixIndexT kdash = N2 - k;
     if (kdash != k) {
       // Next we handle the index k' = N/2 - k.  This is necessary
       // to do now, to avoid invalidating data that we will later need.
       // The quantities C_{k'} and D_{k'} are just the conjugates of C_k
       // and D_k, so the equations are simple modifications of the above,
       // replacing Ck_im and Dk_im with their negatives.
       data[2*kdash] = Ck_re;  // A_k' <-- C_k'
       data[2*kdash+1] = -Ck_im;
       // now A_k' += D_k' 1^(k'/N)
       // We use 1^(k'/N) = 1^((N/2 - k) / N) = 1^(1/2) 1^(-k/N) = -1 * (1^(k/N))^*
       // so it's the same as 1^(k/N) but with the real part negated.
       ComplexAddProduct(Dk_re, -Dk_im, -kN_re, kN_im, &(data[2*kdash]), &(data[2*kdash+1]));
     }
   }
 
   {  // Now handle k = 0.
     // In simple terms: after the complex fft, data[0] becomes the sum of real
     // parts input[0], input[2]... and data[1] becomes the sum of imaginary
     // pats input[1], input[3]...
     // "zeroth" [A_0] is just the sum of input[0]+input[1]+input[2]..
     // and "n2th" [A_{N/2}] is input[0]-input[1]+input[2]... .
     Real zeroth = data[0] + data[1],
         n2th = data[0] - data[1];
     data[0] = zeroth;
     data[1] = n2th;
     if (!forward) {
       data[0] /= 2;
       data[1] /= 2;
     }
   }
 
   if (!forward) {
     ComplexFft(v, false);
     v->Scale(2.0);  // This is so we get a factor of N increase, rather than N/2 which we would
     // otherwise get from [ComplexFft, forward] + [ComplexFft, backward] in dimension N/2.
     // It's for consistency with our normal FFT convensions.
   }
 }

◆ RealFftInefficient()

void RealFftInefficient	(	VectorBase< Real > *	v,
		bool	forward
	)

Inefficient version of Fourier transform, for testing purposes.

RealFt has the same input and output format as RealFft above, but it is an inefficient implementation included for testing purposes.

Definition at line 350 of file matrix-functions.cc.

References kaldi::ComplexFft(), VectorBase< Real >::CopyFromVec(), VectorBase< Real >::Dim(), rnnlm::i, KALDI_ASSERT, and VectorBase< Real >::Range().

Referenced by kaldi::UnitTestRealFft(), and kaldi::UnitTestSplitRadixRealFft().

                                                                                     {
   KALDI_ASSERT(v != NULL);
   MatrixIndexT N = v->Dim();
   KALDI_ASSERT(N%2 == 0);
   if (N == 0) return;
   Vector<Real> vtmp(N*2);  // store as complex.
   if (forward) {
     for (MatrixIndexT i = 0; i < N; i++)  vtmp(i*2) = (*v)(i);
     ComplexFft(&vtmp, forward);  // this is already tested so we can use this.
     v->CopyFromVec( vtmp.Range(0, N) );
     (*v)(1) = vtmp(N);  // Copy the N/2'th fourier component, which is real,
     // to the imaginary part of the 1st complex output.
   } else {
     // reverse the transformation above to get the complex spectrum.
     vtmp(0) = (*v)(0);  // copy F_0 which is real
     vtmp(N) = (*v)(1);  // copy F_{N/2} which is real
     for (MatrixIndexT i = 1; i < N/2; i++) {
       // Copy i'th to i'th fourier component
       vtmp(2*i) = (*v)(2*i);
       vtmp(2*i+1) = (*v)(2*i+1);
       // Copy i'th to N-i'th, conjugated.
       vtmp(2*(N-i)) = (*v)(2*i);
       vtmp(2*(N-i)+1) = -(*v)(2*i+1);
     }
     ComplexFft(&vtmp, forward);  // actually backward since forward == false
     // Copy back real part.  Complex part should be zero.
     for (MatrixIndexT i = 0; i < N; i++)
       (*v)(i) = vtmp(i*2);
   }
 }

◆ SolveDoubleQuadraticMatrixProblem()

Real SolveDoubleQuadraticMatrixProblem	(	const MatrixBase< Real > &	G,
		const SpMatrix< Real > &	P1,
		const SpMatrix< Real > &	P2,
		const SpMatrix< Real > &	Q1,
		const SpMatrix< Real > &	Q2,
		const SolverOptions &	opts,
		MatrixBase< Real > *	M
	)

Maximizes the auxiliary function :

$Q(M) = tr(M^T G) -0.5 tr(P_1 M Q_1 M^T) -0.5 tr(P_2 M Q_2 M^T).$

Encountered in matrix update with a prior.

We also apply a limit on the condition but it should be less frequently necessary, and can be set larger.

Definition at line 827 of file sp-matrix.cc.

References SpMatrix< Real >::AddMat2Sp(), MatrixBase< Real >::AddMatMat(), VectorBase< Real >::AddMatVec(), SpMatrix< Real >::AddSp(), TpMatrix< Real >::Cholesky(), rnnlm::d, TpMatrix< Real >::Invert(), MatrixBase< Real >::Invert(), SpMatrix< Real >::IsDiagonal(), SpMatrix< Real >::IsUnit(), KALDI_ASSERT, KALDI_ERR, KALDI_WARN, kaldi::kNoTrans, kaldi::kTrans, rnnlm::n, SolverOptions::name, MatrixBase< Real >::NumCols(), MatrixBase< Real >::NumRows(), PackedMatrix< Real >::NumRows(), MatrixBase< Real >::Row(), kaldi::SolveQuadraticProblem(), SpMatrix< Real >::SymPosSemiDefEig(), kaldi::VecSpVec(), and kaldi::VecVec().

Referenced by MleAmSgmm2Updater::MapUpdateM(), SolverOptions::SolverOptions(), kaldi::TraceSpSpLower(), and kaldi::UnitTestSolve().

                                                             {
   KALDI_ASSERT(Q1.NumRows() == M->NumCols() && P1.NumRows() == M->NumRows() &&
                G.NumRows() == M->NumRows() && G.NumCols() == M->NumCols() &&
                M->NumCols() != 0 && Q2.NumRows() == M->NumCols() &&
                P2.NumRows() == M->NumRows());
   MatrixIndexT rows = M->NumRows(), cols = M->NumCols();
   // The following check should not fail as we stipulate P1, P2 and one of Q1
   // or Q2 must be +ve def and other Q1 or Q2 must be +ve semidef.
   TpMatrix<Real> LInv(rows);
   LInv.Cholesky(P1);
   LInv.Invert();  // Will throw exception if fails.
   SpMatrix<Real> S(rows);
   Matrix<Real> LInvFull(LInv);
   S.AddMat2Sp(1.0, LInvFull, kNoTrans, P2, 0.0);  // S := L^{-1} P_2 L^{-T}
   Matrix<Real> U(rows, rows);
   Vector<Real> d(rows);
   S.SymPosSemiDefEig(&d, &U);
   Matrix<Real> T(rows, rows);
   T.AddMatMat(1.0, U, kTrans, LInvFull, kNoTrans, 0.0);  // T := U^T * L^{-1}
 
 #ifdef KALDI_PARANOID  // checking mainly for errors in the code or math.
   {
     SpMatrix<Real> P1Trans(rows);
     P1Trans.AddMat2Sp(1.0, T, kNoTrans, P1, 0.0);
     KALDI_ASSERT(P1Trans.IsUnit(0.01));
   }
   {
     SpMatrix<Real> P2Trans(rows);
     P2Trans.AddMat2Sp(1.0, T, kNoTrans, P2, 0.0);
     KALDI_ASSERT(P2Trans.IsDiagonal(0.01));
   }
 #endif
 
   Matrix<Real> TInv(T);
   TInv.Invert();
   Matrix<Real> Gdash(rows, cols);
   Gdash.AddMatMat(1.0, T, kNoTrans, G, kNoTrans, 0.0);  // G' = T G
   Matrix<Real> MdashOld(rows, cols);
   MdashOld.AddMatMat(1.0, TInv, kTrans, *M, kNoTrans, 0.0);  // M' = T^{-T} M
   Matrix<Real> MdashNew(MdashOld);
   Real objf_impr = 0.0;
   for (MatrixIndexT n = 0; n < rows; n++) {
     SpMatrix<Real> Qsum(Q1);
     Qsum.AddSp(d(n), Q2);
     SubVector<Real> mdash_n = MdashNew.Row(n);
     SubVector<Real> gdash_n = Gdash.Row(n);
 
     Matrix<Real> QsumInv(Qsum);
     try {
       QsumInv.Invert();
       Real old_objf = VecVec(mdash_n, gdash_n)
           - 0.5 * VecSpVec(mdash_n, Qsum, mdash_n);
       mdash_n.AddMatVec(1.0, QsumInv, kNoTrans, gdash_n, 0.0); // m'_n := g'_n * (Q_1 + d_n Q_2)^{-1}
       Real new_objf = VecVec(mdash_n, gdash_n)
           - 0.5 * VecSpVec(mdash_n, Qsum, mdash_n);
       if (new_objf < old_objf) {
         if (new_objf < old_objf - 1.0e-05) {
           KALDI_WARN << "In double quadratic matrix problem: objective "
               "function decreasing during optimization of " << opts.name
               << ", " << old_objf << "->" << new_objf << ", change is "
               << (new_objf - old_objf);
           KALDI_ERR << "Auxiliary function decreasing."; // Will be caught.
         } else {  // Reset to old value, didn't improve (very close to optimum).
           MdashNew.Row(n).CopyFromVec(MdashOld.Row(n));
         }
       }
       objf_impr += new_objf - old_objf;
     }
     catch (...) {
       KALDI_WARN << "Matrix inversion or optimization failed during double "
           "quadratic problem, solving for" << opts.name
           << ": trying more stable approach.";
       objf_impr += SolveQuadraticProblem(Qsum, gdash_n, opts, &mdash_n);
     }
   }
   M->AddMatMat(1.0, T, kTrans, MdashNew, kNoTrans, 0.0); // M := T^T M'.
   return objf_impr;
 }

◆ SolveQuadraticMatrixProblem()

Real SolveQuadraticMatrixProblem	(	const SpMatrix< Real > &	Q,
		const MatrixBase< Real > &	Y,
		const SpMatrix< Real > &	P,
		const SolverOptions &	opts,
		MatrixBase< Real > *	M
	)

Maximizes the auxiliary function :

$Q(x) = tr(M^T P Y) - 0.5 tr(P M Q M^T)$

Like a numerically stable version of 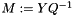$M := Y Q^{-1}$ .

Assumes Q and P positive semidefinite, and matrix dimensions match enough to make expressions meaningful. This is mostly as described in the SGMM paper "the subspace Gaussian mixture model – a structured model for speech recognition", but the diagonal_precondition option is newly added, to handle problems where different dimensions have very different scaling (we recommend to use the option but it's set false for back compatibility).

Definition at line 729 of file sp-matrix.cc.

References MatrixBase< Real >::AddMat(), SpMatrix< Real >::AddMat2Sp(), MatrixBase< Real >::AddMatMat(), SpMatrix< Real >::AddVec2Sp(), VectorBase< Real >::ApplyFloor(), VectorBase< Real >::ApplyPow(), SolverOptions::Check(), VectorBase< Real >::CopyDiagFromSp(), MatrixBase< Real >::CopyFromMat(), SolverOptions::diagonal_precondition, SolverOptions::eps, rnnlm::i, VectorBase< Real >::InvertElements(), SpMatrix< Real >::IsZero(), SolverOptions::K, KALDI_ASSERT, KALDI_LOG, KALDI_WARN, kaldi::kNoTrans, kaldi::kTrans, VectorBase< Real >::Max(), MatrixBase< Real >::MulColsVec(), SolverOptions::name, MatrixBase< Real >::NumCols(), MatrixBase< Real >::NumRows(), PackedMatrix< Real >::NumRows(), SolverOptions::optimize_delta, SolverOptions::print_debug_output, SpMatrix< Real >::SymPosSemiDefEig(), kaldi::TraceMatMat(), and kaldi::TraceSpSp().

Referenced by SolverOptions::SolverOptions(), kaldi::TraceSpSpLower(), kaldi::UnitTestSolve(), EbwAmSgmm2Updater::UpdateM(), MleAmSgmm2Updater::UpdateM(), EbwAmSgmm2Updater::UpdateN(), MleAmSgmm2Updater::UpdateN(), and IvectorExtractorStats::UpdateProjection().

                                                  {
   KALDI_ASSERT(Q.NumRows() == M->NumCols() &&
                SigmaInv.NumRows() == M->NumRows() && Y.NumRows() == M->NumRows()
                && Y.NumCols() == M->NumCols() && M->NumCols() != 0);
   opts.Check();
   MatrixIndexT rows = M->NumRows(), cols = M->NumCols();
   if (Q.IsZero(0.0)) {
     KALDI_WARN << "Zero quadratic term in quadratic matrix problem for "
                << opts.name << ": leaving it unchanged.";
     return 0.0;
   }
 
   if (opts.diagonal_precondition) {
     // We can re-cast the problem with a diagonal preconditioner in the space
     // of Q (columns of M).  Helps to improve the condition of Q.
     Vector<Real> Q_diag(cols);
     Q_diag.CopyDiagFromSp(Q);
     Q_diag.ApplyFloor(std::numeric_limits<Real>::min() * 1.0E+3);
     Vector<Real> Q_diag_sqrt(Q_diag);
     Q_diag_sqrt.ApplyPow(0.5);
     Vector<Real> Q_diag_inv_sqrt(Q_diag_sqrt);
     Q_diag_inv_sqrt.InvertElements();
     Matrix<Real> M_scaled(*M);
     M_scaled.MulColsVec(Q_diag_sqrt);
     Matrix<Real> Y_scaled(Y);
     Y_scaled.MulColsVec(Q_diag_inv_sqrt);
     SpMatrix<Real> Q_scaled(cols);
     Q_scaled.AddVec2Sp(1.0, Q_diag_inv_sqrt, Q, 0.0);
     Real ans;
     SolverOptions new_opts(opts);
     new_opts.diagonal_precondition = false;
     ans = SolveQuadraticMatrixProblem(Q_scaled, Y_scaled, SigmaInv,
                                       new_opts, &M_scaled);
     M->CopyFromMat(M_scaled);
     M->MulColsVec(Q_diag_inv_sqrt);
     return ans;
   }
 
   Matrix<Real> Ybar(Y);
   if (opts.optimize_delta) {
     Matrix<Real> Qfull(Q);
     Ybar.AddMatMat(-1.0, *M, kNoTrans, Qfull, kNoTrans, 1.0);
   } // Ybar = Y - M Q.
   Matrix<Real> U(cols, cols);
   Vector<Real> l(cols);
   Q.SymPosSemiDefEig(&l, &U);  // does svd Q = U L V^T and checks that Q == U L U^T to within a tolerance.
   // floor l.
   Real f = std::max<Real>(static_cast<Real>(opts.eps), l.Max() / opts.K);
   MatrixIndexT nfloored = 0;
   for (MatrixIndexT i = 0; i < cols; i++) {  // floor l.
     if (l(i) < f) { nfloored++; l(i) = f; }
   }
   if (nfloored != 0 && opts.print_debug_output)
     KALDI_LOG << "Solving matrix problem for " << opts.name
               << ": floored " << nfloored << " eigenvalues. ";
   Matrix<Real> tmpDelta(rows, cols);
   tmpDelta.AddMatMat(1.0, Ybar, kNoTrans, U, kNoTrans, 0.0);  // tmpDelta = Ybar * U.
   l.InvertElements(); KALDI_ASSERT(1.0/l.Max() != 0);  // check not infinite.  eps should take care of this.
   tmpDelta.MulColsVec(l);  // tmpDelta = Ybar * U * \tilde{L}^{-1}
 
   Matrix<Real> Delta(rows, cols);
   Delta.AddMatMat(1.0, tmpDelta, kNoTrans, U, kTrans, 0.0);  // Delta = Ybar * U * \tilde{L}^{-1} * U^T
 
   Real auxf_before, auxf_after;
   SpMatrix<Real> MQM(rows);
   Matrix<Real> &SigmaInvY(tmpDelta);
   { Matrix<Real> SigmaInvFull(SigmaInv);  SigmaInvY.AddMatMat(1.0, SigmaInvFull, kNoTrans, Y, kNoTrans, 0.0); }
   {  // get auxf_before.      Q(x) = tr(M^T SigmaInv Y) - 0.5 tr(SigmaInv M Q M^T).
     MQM.AddMat2Sp(1.0, *M, kNoTrans, Q, 0.0);
     auxf_before = TraceMatMat(*M, SigmaInvY, kaldi::kTrans) - 0.5*TraceSpSp(SigmaInv, MQM);
   }
 
   Matrix<Real> Mhat(Delta);
   if (opts.optimize_delta) Mhat.AddMat(1.0, *M);  // Mhat = Delta + M.
 
   {  // get auxf_after.
     MQM.AddMat2Sp(1.0, Mhat, kNoTrans, Q, 0.0);
     auxf_after = TraceMatMat(Mhat, SigmaInvY, kaldi::kTrans) - 0.5*TraceSpSp(SigmaInv, MQM);
   }
 
   if (auxf_after < auxf_before) {
     if (auxf_after < auxf_before - 1.0e-10)
       KALDI_WARN << "Optimizing matrix auxiliary function for "
                  << opts.name << ", auxf decreased "
                  << auxf_before << " to " << auxf_after << ", change is "
                  << (auxf_after-auxf_before);
     return 0.0;
   } else {
     M->CopyFromMat(Mhat);
     return auxf_after - auxf_before;
   }
 }

◆ SolveQuadraticProblem()

Real kaldi::SolveQuadraticProblem	(	const SpMatrix< Real > &	H,
		const VectorBase< Real > &	g,
		const SolverOptions &	opts,
		VectorBase< Real > *	x
	)

Maximizes the auxiliary function

$Q(x) = x.g - 0.5 x^T H x$

using a numerically stable method.

Like a numerically stable version of 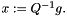$x := Q^{-1} g.$ Assumes H positive semidefinite. Returns the objective-function change.

◆ SortSvd()

void SortSvd	(	VectorBase< Real > *	s,
		MatrixBase< Real > *	U,
		MatrixBase< Real > *	Vt = `NULL`,
		bool	sort_on_absolute_value = `true`
	)

Function to ensure that SVD is sorted.

This function is made as generic as possible, to be applicable to other types of problems. s->Dim() should be the same as U->NumCols(), and we sort s from greatest to least absolute value (if sort_on_absolute_value == true) or greatest to least value otherwise, moving the columns of U, if it exists, and the rows of Vt, if it exists, around in the same way. Note: the "absolute value" part won't matter if this is an actual SVD, since singular values are non-negative.

Makes sure the Svd is sorted (from greatest to least absolute value).

Definition at line 2580 of file kaldi-matrix.cc.

References rnnlm::d, VectorBase< Real >::Dim(), KALDI_ASSERT, MatrixBase< Real >::NumCols(), MatrixBase< Real >::NumRows(), MatrixBase< Real >::Row(), and kaldi::SortSvd().

Referenced by Plda::ApplyTransform(), kaldi::ComputeFeatureNormalizingTransform(), kaldi::ComputeLdaTransform(), kaldi::ComputeNormalizingTransform(), kaldi::ComputePca(), SvdApplier::DecomposeComponent(), LdaEstimate::Estimate(), BasisFmllrEstimate::EstimateFmllrBasis(), FeatureTransformEstimate::EstimateInternal(), kaldi::EstimateSgmm2FmllrSubspace(), kaldi::EstPca(), IvectorExtractorStats::GetOrthogonalIvectorTransform(), PldaEstimator::GetOutput(), AffineComponent::LimitRank(), main(), LimitRankClass::operator()(), OnlineNaturalGradientSimple::PreconditionDirectionsCpu(), OnlinePreconditionerSimple::PreconditionDirectionsCpu(), OnlinePreconditioner::PreconditionDirectionsInternal(), OnlineNaturalGradient::PreconditionDirectionsInternal(), kaldi::nnet3::ReduceRankOfComponents(), SpMatrix< float >::TopEigs(), kaldi::TraceMat(), kaldi::UnitTestPca2(), kaldi::UnitTestSvdNodestroy(), and PldaUnsupervisedAdaptor::UpdatePlda().

                                                                                       {
   MatrixIndexT num_singval = s->Dim();
   KALDI_ASSERT(U == NULL || U->NumCols() == num_singval);
   KALDI_ASSERT(Vt == NULL || Vt->NumRows() == num_singval);
 
   std::vector<std::pair<Real, MatrixIndexT> > vec(num_singval);
   // negative because we want revese order.
   for (MatrixIndexT d = 0; d < num_singval; d++) {
     Real val = (*s)(d),
         sort_val = -(sort_on_absolute_value ? std::abs(val) : val);
     vec[d] = std::pair<Real, MatrixIndexT>(sort_val, d);
   }
   std::sort(vec.begin(), vec.end());
   Vector<Real> s_copy(*s);
   for (MatrixIndexT d = 0; d < num_singval; d++)
     (*s)(d) = s_copy(vec[d].second);
   if (U != NULL) {
     Matrix<Real> Utmp(*U);
     MatrixIndexT dim = Utmp.NumRows();
     for (MatrixIndexT d = 0; d < num_singval; d++) {
       MatrixIndexT oldidx = vec[d].second;
       for (MatrixIndexT e = 0; e < dim; e++)
         (*U)(e, d) = Utmp(e, oldidx);
     }
   }
   if (Vt != NULL) {
     Matrix<Real> Vttmp(*Vt);
     for (MatrixIndexT d = 0; d < num_singval; d++)
       (*Vt).Row(d).CopyFromVec(Vttmp.Row(vec[d].second));
   }
 }

Classes

Functions

Detailed Description

Function Documentation

◆ AddOuterProductPlusMinus()

◆ AssertSameDim()

◆ AttemptComplexPower()

◆ ComplexAddProduct()

◆ ComplexFft()

◆ ComplexFt()

◆ ComplexImExp()

◆ ComplexMul()

◆ ComputeDctMatrix()

◆ ComputePca()

◆ CreateEigenvalueMatrix()

◆ RealFft()

◆ RealFftInefficient()

◆ SolveDoubleQuadraticMatrixProblem()

◆ SolveQuadraticMatrixProblem()

◆ SolveQuadraticProblem()

◆ SortSvd()