mle-diag-gmm-test.cc File Reference

#include "gmm/diag-gmm.h"
#include "gmm/diag-gmm-normal.h"
#include "gmm/mle-diag-gmm.h"
#include "util/kaldi-io.h"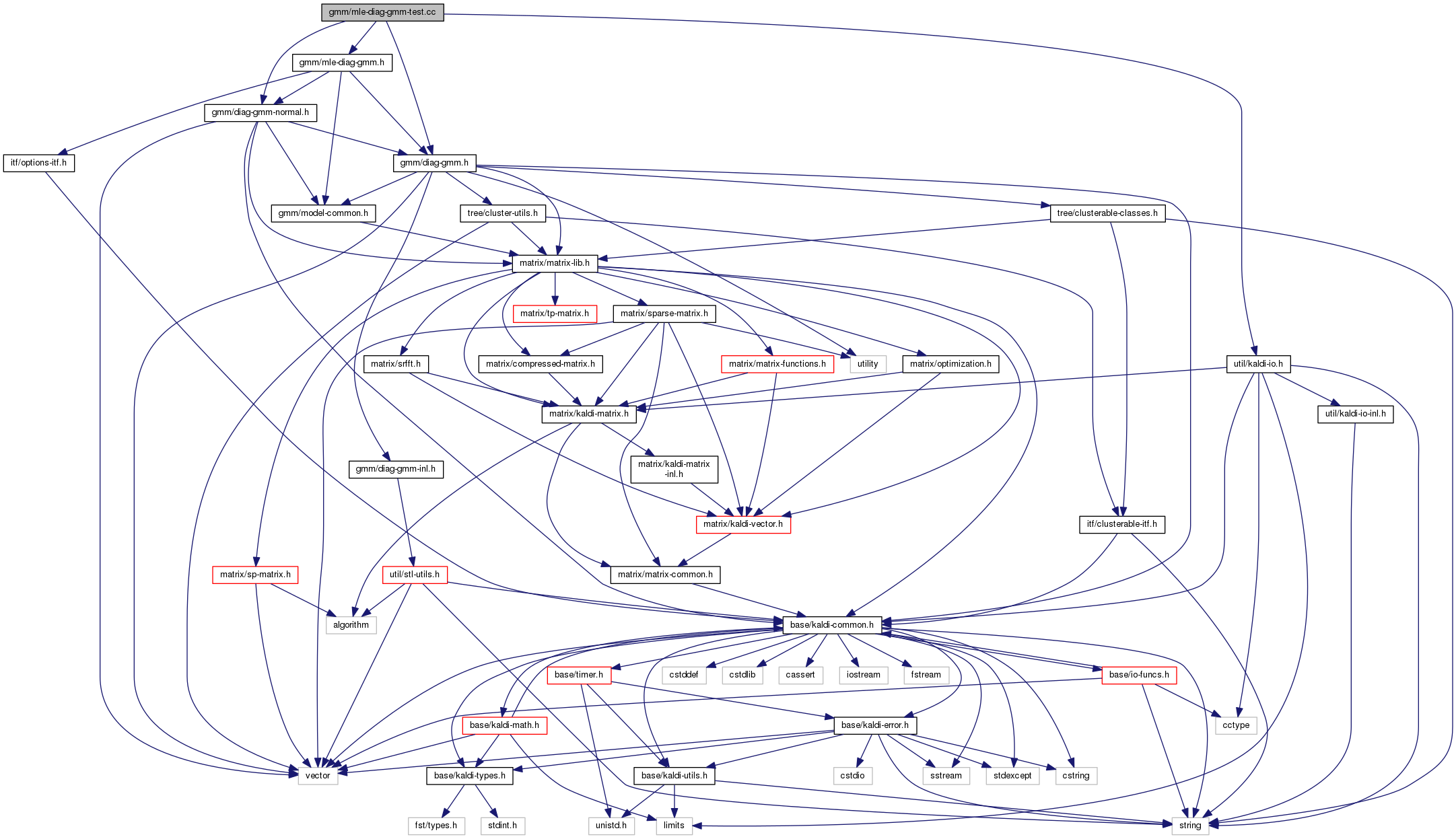

Include dependency graph for mle-diag-gmm-test.cc:

Go to the source code of this file.

Functions
void	TestComponentAcc (const DiagGmm &gmm, const Matrix< BaseFloat > &feats)
void	test_flags_driven_update (const DiagGmm &gmm, const Matrix< BaseFloat > &feats, GmmFlagsType flags)
void	test_io (const DiagGmm &gmm, const AccumDiagGmm &est_gmm, bool binary, const Matrix< BaseFloat > &feats)
void	UnitTestEstimateDiagGmm ()
int	main ()

Function Documentation

main()

int main

(

)

Definition at line 407 of file mle-diag-gmm-test.cc.

References rnnlm::i, and UnitTestEstimateDiagGmm().

           {
  // repeat the test five times
  for (int i = 0; i < 2; i++)
    UnitTestEstimateDiagGmm();
  std::cout << "Test OK.\n";
}

test_flags_driven_update()

void test_flags_driven_update	(	const DiagGmm &	gmm,
		const Matrix< BaseFloat > &	feats,
		GmmFlagsType	flags
	)

Definition at line 87 of file mle-diag-gmm-test.cc.

References AccumDiagGmm::AccumulateFromDiag(), kaldi::AssertEqual(), DiagGmm::ComputeGconsts(), DiagGmm::CopyFromDiagGmm(), DiagGmm::Dim(), DiagGmm::GetMeans(), DiagGmm::GetVars(), rnnlm::i, KALDI_WARN, kaldi::kGmmAll, kaldi::kGmmMeans, kaldi::kGmmVariances, kaldi::kGmmWeights, DiagGmm::LogLikelihood(), kaldi::MleDiagGmmUpdate(), DiagGmm::NumGauss(), AccumDiagGmm::NumGauss(), MatrixBase< Real >::NumRows(), AccumDiagGmm::Resize(), MatrixBase< Real >::Row(), DiagGmm::SetInvVars(), DiagGmm::SetMeans(), DiagGmm::SetWeights(), AccumDiagGmm::SetZero(), and DiagGmm::weights().

Referenced by UnitTestEstimateDiagGmm().

                                                  {
  MleDiagGmmOptions config;
  AccumDiagGmm est_gmm_allp;   // updates all params
  // let's trust that all-params update works
  AccumDiagGmm est_gmm_somep;  // updates params indicated by flags

  // warm-up estimators
  est_gmm_allp.Resize(gmm.NumGauss(),
    gmm.Dim(), kGmmAll);
  est_gmm_allp.SetZero(kGmmAll);
  est_gmm_somep.Resize(gmm.NumGauss(),
    gmm.Dim(), flags);
  est_gmm_somep.SetZero(flags);

  // accumulate estimators
  for (int32 i = 0; i < feats.NumRows(); i++) {
    est_gmm_allp.AccumulateFromDiag(gmm, feats.Row(i), 1.0F);
    est_gmm_somep.AccumulateFromDiag(gmm, feats.Row(i), 1.0F);
  }

  DiagGmm gmm_all_update;   // model with all params updated
  DiagGmm gmm_some_update;  // model with some params updated
  gmm_all_update.CopyFromDiagGmm(gmm);   // init with orig. model
  gmm_some_update.CopyFromDiagGmm(gmm);  // init with orig. model

  MleDiagGmmUpdate(config, est_gmm_allp, kGmmAll, &gmm_all_update, NULL, NULL);
  MleDiagGmmUpdate(config, est_gmm_somep, flags, &gmm_some_update, NULL, NULL);

  if (est_gmm_allp.NumGauss() != gmm.NumGauss()) {
    KALDI_WARN << "Unable to pass test_update_flags() test because of "
      "component removal during Update() call (this is normal)";
    return;
  }

  // now back-off the gmm_all_update params that were not updated
  // in gmm_some_update to orig.
  if (~flags & kGmmWeights)
    gmm_all_update.SetWeights(gmm.weights());
  if (~flags & kGmmMeans) {
    Matrix<BaseFloat> means(gmm.NumGauss(), gmm.Dim());
    gmm.GetMeans(&means);
    gmm_all_update.SetMeans(means);
  }
  if (~flags & kGmmVariances) {
    Matrix<BaseFloat> vars(gmm.NumGauss(), gmm.Dim());
    gmm.GetVars(&vars);
    vars.InvertElements();
    gmm_all_update.SetInvVars(vars);
  }
  gmm_all_update.ComputeGconsts();

  // now both models gmm_all_update, gmm_all_update have the same params updated
  // compute loglike for models for check
  double loglike0 = 0.0;
  double loglike1 = 0.0;
  double loglike2 = 0.0;
  for (int32 i = 0; i < feats.NumRows(); i++) {
    loglike0 += static_cast<double>(
      gmm.LogLikelihood(feats.Row(i)));
    loglike1 += static_cast<double>(
      gmm_all_update.LogLikelihood(feats.Row(i)));
    loglike2 += static_cast<double>(
      gmm_some_update.LogLikelihood(feats.Row(i)));
  }
  if ((flags & kGmmVariances) && !(flags & kGmmMeans))
    return;  // Don't run the test as the variance update gives a different
  // answer if you don't update the mean.

  AssertEqual(loglike1, loglike2, 1.0e-6);
}

test_io()

void test_io	(	const DiagGmm &	gmm,
		const AccumDiagGmm &	est_gmm,
		bool	binary,
		const Matrix< BaseFloat > &	feats
	)

Definition at line 161 of file mle-diag-gmm-test.cc.

References kaldi::AssertEqual(), DiagGmm::CopyFromDiagGmm(), AccumDiagGmm::Dim(), AccumDiagGmm::Flags(), rnnlm::i, kaldi::kGmmAll, DiagGmm::LogLikelihood(), kaldi::MleDiagGmmUpdate(), AccumDiagGmm::NumGauss(), MatrixBase< Real >::NumRows(), AccumDiagGmm::Read(), AccumDiagGmm::Resize(), MatrixBase< Real >::Row(), AccumDiagGmm::Scale(), Input::Stream(), and AccumDiagGmm::Write().

Referenced by UnitTestEstimateDiagGmm().

                                        {
  std::cout << "Testing I/O, binary = " << binary << '\n';

  est_gmm.Write(Output("tmp_stats", binary).Stream(), binary);

  bool binary_in;
  AccumDiagGmm est_gmm2;
  est_gmm2.Resize(est_gmm.NumGauss(),
    est_gmm.Dim(), kGmmAll);
  Input ki("tmp_stats", &binary_in);
  est_gmm2.Read(ki.Stream(), binary_in, false);  // not adding

  Input ki2("tmp_stats", &binary_in);
  est_gmm2.Read(ki2.Stream(), binary_in, true);  // adding

  est_gmm2.Scale(0.5, kGmmAll);
    // 0.5 -> make it same as what it would have been if we read just once.
    // [may affect it due to removal of components with small counts].

  MleDiagGmmOptions config;
  DiagGmm gmm1;
  DiagGmm gmm2;
  gmm1.CopyFromDiagGmm(gmm);
  gmm2.CopyFromDiagGmm(gmm);
  MleDiagGmmUpdate(config, est_gmm, est_gmm.Flags(), &gmm1, NULL, NULL);
  MleDiagGmmUpdate(config, est_gmm2, est_gmm2.Flags(), &gmm2, NULL, NULL);

  BaseFloat loglike1 = 0.0;
  BaseFloat loglike2 = 0.0;
  for (int32 i = 0; i < feats.NumRows(); i++) {
    loglike1 += gmm1.LogLikelihood(feats.Row(i));
    loglike2 += gmm2.LogLikelihood(feats.Row(i));
  }

  AssertEqual(loglike1, loglike2, 1.0e-6);

  unlink("tmp_stats");
}

TestComponentAcc()

void TestComponentAcc	(	const DiagGmm &	gmm,
		const Matrix< BaseFloat > &	feats
	)

Definition at line 28 of file mle-diag-gmm-test.cc.

References AccumDiagGmm::AccumulateForComponent(), AccumDiagGmm::AccumulateFromDiag(), kaldi::AssertEqual(), DiagGmm::ComponentPosteriors(), DiagGmm::Dim(), rnnlm::i, KALDI_ASSERT, KALDI_WARN, kaldi::kGmmAll, DiagGmm::LogLikelihood(), kaldi::MleDiagGmmUpdate(), DiagGmm::NumGauss(), AccumDiagGmm::NumGauss(), MatrixBase< Real >::NumRows(), DiagGmm::Resize(), AccumDiagGmm::Resize(), MatrixBase< Real >::Row(), and AccumDiagGmm::SetZero().

Referenced by UnitTestEstimateDiagGmm().

                                                                          {
  MleDiagGmmOptions config;
  AccumDiagGmm est_atonce;    // updates all components
  AccumDiagGmm est_compwise;  // updates single components

  // Initialize estimators
  est_atonce.Resize(gmm.NumGauss(), gmm.Dim(), kGmmAll);
  est_atonce.SetZero(kGmmAll);
  est_compwise.Resize(gmm.NumGauss(),
      gmm.Dim(), kGmmAll);
  est_compwise.SetZero(kGmmAll);

  // accumulate estimators
  for (int32 i = 0; i < feats.NumRows(); i++) {
    est_atonce.AccumulateFromDiag(gmm, feats.Row(i), 1.0F);
    Vector<BaseFloat> post(gmm.NumGauss());
    gmm.ComponentPosteriors(feats.Row(i), &post);
    for (int32 m = 0; m < gmm.NumGauss(); m++) {
      est_compwise.AccumulateForComponent(feats.Row(i), m, post(m));
    }
  }

  DiagGmm gmm_atonce;    // model with all components accumulated together
  DiagGmm gmm_compwise;  // model with each component accumulated separately
  gmm_atonce.Resize(gmm.NumGauss(), gmm.Dim());
  gmm_compwise.Resize(gmm.NumGauss(), gmm.Dim());

  MleDiagGmmUpdate(config, est_atonce, kGmmAll, &gmm_atonce, NULL, NULL);
  MleDiagGmmUpdate(config, est_compwise, kGmmAll, &gmm_compwise, NULL, NULL);

  // the two ways of updating should result in the same model
  double loglike0 = 0.0;
  double loglike1 = 0.0;
  double loglike2 = 0.0;
  for (int32 i = 0; i < feats.NumRows(); i++) {
    loglike0 += static_cast<double>(gmm.LogLikelihood(feats.Row(i)));
    loglike1 += static_cast<double>(gmm_atonce.LogLikelihood(feats.Row(i)));
    loglike2 += static_cast<double>(gmm_compwise.LogLikelihood(feats.Row(i)));
  }

  std::cout << "Per-frame log-likelihood before update = "
      << (loglike0/feats.NumRows()) << '\n';
  std::cout << "Per-frame log-likelihood (accumulating at once) = "
      << (loglike1/feats.NumRows()) << '\n';
  std::cout << "Per-frame log-likelihood (accumulating component-wise) = "
      << (loglike2/feats.NumRows()) << '\n';

  AssertEqual(loglike1, loglike2, 1.0e-6);

  if (est_atonce.NumGauss() != gmm.NumGauss()) {
    KALDI_WARN << "Unable to pass test_update_flags() test because of "
      "component removal during Update() call (this is normal)";
    return;
  } else {
    KALDI_ASSERT(loglike1 >= loglike0 - (std::abs(loglike1)+std::abs(loglike0))*1.0e-06);
    KALDI_ASSERT(loglike2 >= loglike0 - (std::abs(loglike2)+std::abs(loglike0))*1.0e-06);
  }
}

UnitTestEstimateDiagGmm()

void UnitTestEstimateDiagGmm

(

)

Definition at line 202 of file mle-diag-gmm-test.cc.

References AccumDiagGmm::AccumulateFromDiag(), AccumDiagGmm::AccumulateFromDiagMultiThreaded(), VectorBase< Real >::AddVec(), VectorBase< Real >::AddVec2(), VectorBase< Real >::ApplyPow(), kaldi::ApproxEqual(), AccumDiagGmm::AssertEqual(), kaldi::AssertEqual(), DiagGmm::ComputeGconsts(), MatrixBase< Real >::CopyFromMat(), VectorBase< Real >::CopyRowFromMat(), DiagGmmNormal::CopyToDiagGmm(), count, rnnlm::d, DiagGmm::Dim(), kaldi::Exp(), rnnlm::i, DiagGmm::inv_vars(), MatrixBase< Real >::InvertElements(), KALDI_ASSERT, KALDI_LOG, kaldi::kGmmAll, kaldi::kGmmMeans, kaldi::kGmmVariances, kaldi::kGmmWeights, DiagGmmNormal::means_, DiagGmm::means_invvars(), MleDiagGmmOptions::min_variance, kaldi::MleDiagGmmUpdate(), DiagGmm::NumGauss(), kaldi::Rand(), kaldi::RandGauss(), AccumDiagGmm::Read(), DiagGmm::Resize(), AccumDiagGmm::Resize(), MatrixBase< Real >::Row(), VectorBase< Real >::Scale(), DiagGmm::SetInvVarsAndMeans(), DiagGmm::SetWeights(), AccumDiagGmm::SetZero(), DiagGmm::Split(), Input::Stream(), test_flags_driven_update(), test_io(), TestComponentAcc(), DiagGmmNormal::vars_, DiagGmm::weights(), and AccumDiagGmm::Write().

Referenced by main().

                          {
  size_t dim = 15;  // dimension of the gmm
  size_t nMix = 9;  // number of mixtures in the data
  size_t maxiterations = 20;  // number of iterations for estimation

  // maximum number of densities in the GMM
  // larger than the number of mixtures in the data
  // so that we can test the removal of unseen components
  int32 maxcomponents = 10;

  // generate random feature vectors
  Matrix<BaseFloat> means_f(nMix, dim), vars_f(nMix, dim);
  // first, generate random mean and variance vectors
  for (size_t m = 0; m < nMix; m++) {
    for (size_t d= 0; d < dim; d++) {
      means_f(m, d) = kaldi::RandGauss()*100.0F;
      vars_f(m, d) = Exp(kaldi::RandGauss())*1000.0F+ 1.0F;
    }
//    std::cout << "Gauss " << m << ": Mean = " << means_f.Row(m) << '\n'
//        << "Vars = " << vars_f.Row(m) << '\n';
  }
  // second, generate 1000 feature vectors for each of the mixture components
  size_t counter = 0, multiple = 200;
  Matrix<BaseFloat> feats(nMix*multiple, dim);
  for (size_t m = 0; m < nMix; m++) {
    for (size_t i = 0; i < multiple; i++) {
      for (size_t d = 0; d < dim; d++) {
        feats(counter, d) = means_f(m, d) + kaldi::RandGauss() *
            std::sqrt(vars_f(m, d));
      }
      counter++;
    }
  }
  // Compute the global mean and variance
  Vector<BaseFloat> mean_acc(dim);
  Vector<BaseFloat> var_acc(dim);
  Vector<BaseFloat> featvec(dim);
  for (size_t i = 0; i < counter; i++) {
    featvec.CopyRowFromMat(feats, i);
    mean_acc.AddVec(1.0, featvec);
    featvec.ApplyPow(2.0);
    var_acc.AddVec(1.0, featvec);
  }
  mean_acc.Scale(1.0F/counter);
  var_acc.Scale(1.0F/counter);
  var_acc.AddVec2(-1.0, mean_acc);
//  std::cout << "Mean acc = " << mean_acc << '\n' << "Var acc = "
//      << var_acc << '\n';

  // write the feature vectors to a file
  //  std::ofstream of("tmpfeats");
  //  of.precision(10);
  //  of << feats;
  //  of.close();

  // now generate randomly initial values for the GMM
  Vector<BaseFloat> weights(1);
  Matrix<BaseFloat> means(1, dim), vars(1, dim), invvars(1, dim);
  for (size_t d= 0; d < dim; d++) {
    means(0, d) = kaldi::RandGauss()*100.0F;
    vars(0, d) = Exp(kaldi::RandGauss()) *10.0F + 1e-5F;
  }
  weights(0) = 1.0F;
  invvars.CopyFromMat(vars);
  invvars.InvertElements();

  // new GMM
  DiagGmm *gmm = new DiagGmm();
  gmm->Resize(1, dim);
  gmm->SetWeights(weights);
  gmm->SetInvVarsAndMeans(invvars, means);
  gmm->ComputeGconsts();

  {
    KALDI_LOG << "Testing natural<>normal conversion";
    DiagGmmNormal ngmm(*gmm);
    DiagGmm rgmm;
    rgmm.Resize(1, dim);
    ngmm.CopyToDiagGmm(&rgmm);

    // check contents
    KALDI_ASSERT(ApproxEqual(weights(0), 1.0F, 1e-6));
    KALDI_ASSERT(ApproxEqual(gmm->weights()(0), rgmm.weights()(0), 1e-6));
    for (int32 d = 0; d < dim; d++) {
      KALDI_ASSERT(ApproxEqual(means.Row(0)(d), ngmm.means_.Row(0)(d), 1e-6));
      KALDI_ASSERT(ApproxEqual(1./invvars.Row(0)(d), ngmm.vars_.Row(0)(d), 1e-6));
      KALDI_ASSERT(ApproxEqual(gmm->means_invvars().Row(0)(d), rgmm.means_invvars().Row(0)(d), 1e-6));
      KALDI_ASSERT(ApproxEqual(gmm->inv_vars().Row(0)(d), rgmm.inv_vars().Row(0)(d), 1e-6));
    }
    KALDI_LOG << "OK";
  }

  AccumDiagGmm est_gmm;
//  var_acc.Scale(0.1);
//  est_gmm.config_.p_variance_floor_vector = &var_acc;

  MleDiagGmmOptions  config;
  config.min_variance = 0.01;
  GmmFlagsType flags = kGmmAll;  // Should later try reducing this.

  est_gmm.Resize(gmm->NumGauss(), gmm->Dim(), flags);

  // iterate
  size_t iteration = 0;
  float lastloglike = 0.0;
  int32 lastloglike_nM = 0;

  while (iteration < maxiterations) {
    Vector<BaseFloat> featvec(dim);
    est_gmm.Resize(gmm->NumGauss(), gmm->Dim(), flags);
    est_gmm.SetZero(flags);
    double loglike = 0.0;
    for (size_t i = 0; i < counter; i++) {
      featvec.CopyRowFromMat(feats, i);
      loglike += static_cast<double>(est_gmm.AccumulateFromDiag(*gmm,
        featvec, 1.0F));
    }
    std::cout << "Loglikelihood before iteration " << iteration << " : "
        << std::scientific << loglike << " number of components: "
        << gmm->NumGauss() << '\n';

    // every 5th iteration check loglike change and update lastloglike
    if (iteration % 5 == 0) {
      // likelihood should be increasing on the long term
      if ((iteration > 0) && (gmm->NumGauss() >= lastloglike_nM)) {
        KALDI_ASSERT(loglike - lastloglike >= -1.0);
      }
      lastloglike = loglike;
      lastloglike_nM = gmm->NumGauss();
    }

    // binary write
    est_gmm.Write(Output("tmp_stats", true).Stream(), true);

    // binary read
    bool binary_in;
    Input ki("tmp_stats", &binary_in);
    est_gmm.Read(ki.Stream(), binary_in, false);  // false = not adding.

    BaseFloat obj, count;
    MleDiagGmmUpdate(config, est_gmm, flags, gmm, &obj, &count);
    KALDI_LOG <<"ML objective function change = " << (obj/count)
              << " per frame, over " << (count) << " frames.";

    if ((iteration % 3 == 1) && (gmm->NumGauss() * 2 <= maxcomponents)) {
      gmm->Split(gmm->NumGauss() * 2, 0.001);
    }

    if (iteration == 5) {  // run following tests with not too overfitted model
      std::cout << "Testing flags-driven updates" << '\n';
      test_flags_driven_update(*gmm, feats, kGmmAll);
      test_flags_driven_update(*gmm, feats, kGmmWeights);
      test_flags_driven_update(*gmm, feats, kGmmMeans);
      test_flags_driven_update(*gmm, feats, kGmmVariances);
      test_flags_driven_update(*gmm, feats, kGmmWeights | kGmmMeans);
      std::cout << "Testing component-wise accumulation" << '\n';
      TestComponentAcc(*gmm, feats);
    }

    iteration++;
  }

  {  // I/O tests
    GmmFlagsType flags_all = kGmmAll;
    est_gmm.Resize(gmm->NumGauss(),
      gmm->Dim(), flags_all);
    est_gmm.SetZero(flags_all);
    float loglike = 0.0;
    for (size_t i = 0; i < counter; i++) {
      loglike += est_gmm.AccumulateFromDiag(*gmm, feats.Row(i), 1.0F);
    }
    test_io(*gmm, est_gmm, false, feats);  // ASCII mode
    test_io(*gmm, est_gmm, true, feats);   // Binary mode
  }

  { // Test multi-threaded update.
    GmmFlagsType flags_all = kGmmAll;
    est_gmm.Resize(gmm->NumGauss(),
      gmm->Dim(), flags_all);
    est_gmm.SetZero(flags_all);

    Vector<BaseFloat> weights(counter);
    for (size_t i = 0; i < counter; i++)
      weights(i) = 0.5 + 0.1 * (Rand() % 10);


    float loglike = 0.0;
    for (size_t i = 0; i < counter; i++) {
      loglike += weights(i) *
          est_gmm.AccumulateFromDiag(*gmm, feats.Row(i), weights(i));
    }
    AccumDiagGmm est_gmm2(*gmm, flags_all);
    int32 num_threads = 2;
    float loglike2 =
        est_gmm2.AccumulateFromDiagMultiThreaded(*gmm, feats, weights, num_threads);
    AssertEqual(loglike, loglike2);
    est_gmm.AssertEqual(est_gmm2);
  }


  delete gmm;

  unlink("tmp_stats");
}