Class for computing a feature transform used for preconditioning of the training data in neural-networks. More...

#include <get-feature-transform.h>

Inheritance diagram for FeatureTransformEstimate:

Collaboration diagram for FeatureTransformEstimate:

[legend]

Public Member Functions
void	Estimate (const FeatureTransformEstimateOptions &opts, Matrix< BaseFloat > M, TpMatrix< BaseFloat > within_cholesky) const
	Estimates the LDA transform matrix m. More...

Public Member Functions inherited from LdaEstimate
	LdaEstimate ()

void	Init (int32 num_classes, int32 dimension)
	Allocates memory for accumulators. More...

int32	NumClasses () const
	Returns the number of classes. More...

int32	Dim () const
	Returns the dimensionality of the feature vectors. More...

void	ZeroAccumulators ()
	Sets all accumulators to zero. More...

void	Scale (BaseFloat f)
	Scales all accumulators. More...

double	TotCount ()
	Return total count of the data. More...

void	Accumulate (const VectorBase< BaseFloat > &data, int32 class_id, BaseFloat weight=1.0)
	Accumulates data. More...

void	Estimate (const LdaEstimateOptions &opts, Matrix< BaseFloat > M, Matrix< BaseFloat > Mfull=NULL) const
	Estimates the LDA transform matrix m. More...

void	Read (std::istream &in_stream, bool binary, bool add)

void	Write (std::ostream &out_stream, bool binary) const

Static Protected Member Functions
static void	EstimateInternal (const FeatureTransformEstimateOptions &opts, const SpMatrix< double > &total_covar, const SpMatrix< double > &between_covar, const Vector< double > &mean, Matrix< BaseFloat > M, TpMatrix< BaseFloat > C)

Static Protected Member Functions inherited from LdaEstimate
static void	AddMeanOffset (const VectorBase< double > &total_mean, Matrix< BaseFloat > *projection)
	This function modifies the LDA matrix so that it also subtracts the mean feature value. More...

Additional Inherited Members
Protected Member Functions inherited from LdaEstimate
void	GetStats (SpMatrix< double > total_covar, SpMatrix< double > between_covar, Vector< double > total_mean, double sum) const
	Extract a more processed form of the stats. More...

LdaEstimate &	operator= (const LdaEstimate &other)

Protected Attributes inherited from LdaEstimate
Vector< double >	zero_acc_

Matrix< double >	first_acc_

SpMatrix< double >	total_second_acc_

Detailed Description

Class for computing a feature transform used for preconditioning of the training data in neural-networks.

By preconditioning here, all we really mean is an affine transform of the input data– say if we set up the classification as going from vectors x_i to labels y_i, then this would be a linear transform on X, so we replace x_i with x'_i = A x_i + b. The statistics we use to obtain this transform are the within-class and between class variance statistics, and the global data mean, that we would use to estimate LDA. When designing this, we had a few principles in mind:

We want to remove the global mean of the input features (this is well established, I think there is a paper by LeCun explaining why this is a good thing).
We would like the transform to make the training process roughly invariant to linear transformations of the input features, meaning that whatever linear transformation you apply prior to this transform, it should 'undo' it.
We want directions in which there is a lot of between-class variance to be given a higher variance than directions that have mostly within-class variance– it has been our experience that these 'nuisance directions' will interfere with the training if they are given too large a scaling. It is essential to our method that the number of classes is higher than the dimension of the input feature space, which is normal for speech recognition tasks (~5000 > ~250).

Basically our method is as follows:

First subtract the mean.
Get the within-class and between-class stats, as for LDA.
Normalize the space as for LDA, so that the within-class covariance matrix is unit and the between-class covariance matrix is diagonalized
At this stage, if the user asked for dimension reduction then reduce the dimension by taking out dimensions with least between-class variance [note: the current scripts do not do this by default]
Apply a transform that reduces the variance of dimensions with low between-class variance, as we'll describe below.
Finally, do an SVD of the resulting transform, A = U S V^T, apply a maximum to the diagonal elements of the matrix S (e.g. 5.0), and reconstruct A' = U S' V^T; this is the final transform. The point of this stage is to stop the transform from 'blowing up' any dimensions of the space excessively; this stage was introduced in response to a problem we encountered at one point, and I think normally not very many dimensions of S end up getting floored.

We need to explain the step that applies the dimension-specific scaling, which we described above as, "Apply a transform that reduces the variance of dimensions with low between-class variance". For a particular dimension, let the between-class diagonal covariance element be , and the within-class diagonal covariance is 1 at this point (since we have normalized the within-class covariance to unity); hence, the total variance is + 1. Below, "within-class-factor" is a constant that we set by default to 0.001. We scale the i'th dimension of the features by:

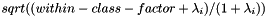
$sqrt( (within-class-factor + \lambda_i) / (1 + \lambda_i) )$

If >> 1, this scaling factor approaches 1 (we don't need to scale up dimensions with high between-class variance as they already naturally have a higher variance than other dimensions. As becomes small, this scaling factor approaches sqrt(within-class-factor), so dimensions with very small between-class variance get assigned a small variance equal to within-class-factor, and for dimensions with intermediate between-class variance, they end up with a variance roughly equal to : consider that the variance was originally (1 + ), so by scaling the features by approximately sqrt(() / (1 + )), the variance becomes approximately [this is clear after noting that the variance gets scaled by the square of the feature scale].

Definition at line 133 of file get-feature-transform.h.

Member Function Documentation

◆ Estimate()

void Estimate	(	const FeatureTransformEstimateOptions &	opts,
		Matrix< BaseFloat > *	M,
		TpMatrix< BaseFloat > *	within_cholesky
	)		const

Estimates the LDA transform matrix m.

If Mfull != NULL, it also outputs the full matrix (without dimensionality reduction), which is useful for some purposes. If opts.remove_offset == true, it will output both matrices with an extra column which corresponds to mean-offset removal (the matrix should be multiplied by the feature with a 1 appended to give the correct result, as with other Kaldi transforms.) "within_cholesky" is a pointer to an SpMatrix that, if non-NULL, will be set to the Cholesky factor of the within-class covariance matrix. This is used for perturbing features.

Definition at line 28 of file get-feature-transform.cc.

References count, FeatureTransformEstimate::EstimateInternal(), LdaEstimate::GetStats(), and KALDI_LOG.

Referenced by main().

                                                                       { 
   double count;
   Vector<double> total_mean;
   SpMatrix<double> total_covar, between_covar;
   GetStats(&total_covar, &between_covar, &total_mean, &count);
   KALDI_LOG << "Data count is " << count;
   EstimateInternal(opts, total_covar, between_covar, total_mean, M, C);
 }

◆ EstimateInternal()

void EstimateInternal	(	const FeatureTransformEstimateOptions &	opts,
		const SpMatrix< double > &	total_covar,
		const SpMatrix< double > &	between_covar,
		const Vector< double > &	mean,
		Matrix< BaseFloat > *	M,
		TpMatrix< BaseFloat > *	C
	)

staticprotected

Definition at line 40 of file get-feature-transform.cc.

Referenced by FeatureTransformEstimate::Estimate(), and FeatureTransformEstimateMulti::EstimateTransformPart().

                             {
   
   int32 target_dim = opts.dim, dim = total_covar.NumRows();
   // Interpret zero or negative target_dim as the full dim
   if (target_dim <= 0)
     target_dim = dim;
   // between-class covar is of most rank C-1
   KALDI_ASSERT(target_dim <= dim);
   
   // within-class covariance
   SpMatrix<double> wc_covar(total_covar);
   wc_covar.AddSp(-1.0, between_covar);
   TpMatrix<double> wc_covar_sqrt(dim);
   try {
     wc_covar_sqrt.Cholesky(wc_covar);
     if (C != NULL) {
       C->Resize(dim);
       C->CopyFromTp(wc_covar_sqrt);
     }
   } catch (...) {
     BaseFloat smooth = 1.0e-03 * wc_covar.Trace() / wc_covar.NumRows();
     KALDI_LOG << "Cholesky failed (possibly not +ve definite), so adding " << smooth
               << " to diagonal and trying again.\n";
     for (int32 i = 0; i < wc_covar.NumRows(); i++)
       wc_covar(i, i) += smooth;
     wc_covar_sqrt.Cholesky(wc_covar);    
   }
   Matrix<double> wc_covar_sqrt_mat(wc_covar_sqrt);
   wc_covar_sqrt_mat.Invert();
 
   SpMatrix<double> tmp_sp(dim);
   tmp_sp.AddMat2Sp(1.0, wc_covar_sqrt_mat, kNoTrans, between_covar, 0.0);
   Matrix<double> tmp_mat(tmp_sp);
   Matrix<double> svd_u(dim, dim), svd_vt(dim, dim);
   Vector<double> svd_d(dim);
   tmp_mat.Svd(&svd_d, &svd_u, &svd_vt);
   SortSvd(&svd_d, &svd_u);
 
   KALDI_LOG << "LDA singular values are " << svd_d;
 
   KALDI_LOG << "Sum of all singular values is " << svd_d.Sum();
   KALDI_LOG << "Sum of selected singular values is " <<
       SubVector<double>(svd_d, 0, target_dim).Sum();
   
   Matrix<double> lda_mat(dim, dim);
   lda_mat.AddMatMat(1.0, svd_u, kTrans, wc_covar_sqrt_mat, kNoTrans, 0.0);
 
   // finally, copy first target_dim rows to m
   M->Resize(target_dim, dim);
   M->CopyFromMat(lda_mat.Range(0, target_dim, 0, dim));
   
   if (opts.within_class_factor != 1.0) {
     for (int32 i = 0; i < svd_d.Dim(); i++) {
       BaseFloat old_var = 1.0 + svd_d(i), // the total variance of that dim..
           new_var = opts.within_class_factor + svd_d(i), // the variance we want..
           scale = sqrt(new_var / old_var);
       if (i < M->NumRows())
         M->Row(i).Scale(scale);
     }
   }
 
   if (opts.max_singular_value > 0.0) {
     int32 rows = M->NumRows(), cols = M->NumCols(),
         min_dim = std::min(rows, cols);
     Matrix<BaseFloat> U(rows, min_dim), Vt(min_dim, cols);
     Vector<BaseFloat> s(min_dim);
     M->Svd(&s, &U, &Vt); // decompose m = U diag(s) Vt.
     BaseFloat max_s = s.Max();
     int32 n;
     s.ApplyCeiling(opts.max_singular_value, &n);
     if (n > 0) {
       KALDI_LOG << "Applied ceiling to " << n << " out of " << s.Dim()
                 << " singular values of transform using ceiling "
                 << opts.max_singular_value << ", max is " << max_s;
       Vt.MulRowsVec(s);
       // reconstruct m with the modified singular values:
       M->AddMatMat(1.0, U, kNoTrans, Vt, kNoTrans, 0.0);
     }
   }
 
   if (opts.remove_offset)
     AddMeanOffset(total_mean, M);
 }

The documentation for this class was generated from the following files:

nnet2/get-feature-transform.h
nnet2/get-feature-transform.cc

Public Member Functions

Static Protected Member Functions

Additional Inherited Members

Detailed Description

Member Function Documentation

◆ Estimate()

◆ EstimateInternal()