371 Real rootN_re, rootN_im;
372 int forward_sign = forward ? -1 : 1;
374 Real kN_re = -forward_sign, kN_im = 0.0;
377 ComplexMul(rootN_re, rootN_im, &kN_re, &kN_im);
379 Real Ck_re, Ck_im, Dk_re, Dk_im;
381 Ck_re = 0.5 * (data[2*k] + data[N - 2*k]);
382 Ck_im = 0.5 * (data[2*k + 1] - data[N - 2*k + 1]);
384 Dk_re = 0.5 * (data[2*k + 1] + data[N - 2*k + 1]);
386 Dk_im =-0.5 * (data[2*k] - data[N - 2*k]);
400 data[2*kdash] = Ck_re;
401 data[2*kdash+1] = -Ck_im;
405 ComplexAddProduct(Dk_re, -Dk_im, -kN_re, kN_im, &(data[2*kdash]), &(data[2*kdash+1]));
415 Real zeroth = data[0] + data[1],
416 n2th = data[0] - data[1];
void Compute(Real *xr, Real *xi, bool forward) const
void ComplexAddProduct(const Real &a_re, const Real &a_im, const Real &b_re, const Real &b_im, Real *c_re, Real *c_im)
ComplexMul implements, inline, the complex operation c += (a * b).
void ComplexMul(const Real &a_re, const Real &a_im, Real *b_re, Real *b_im)
ComplexMul implements, inline, the complex multiplication b *= a.
#define KALDI_ASSERT(cond)
void ComplexImExp(Real x, Real *a_re, Real *a_im)
ComplexImExp implements a <– exp(i x), inline.
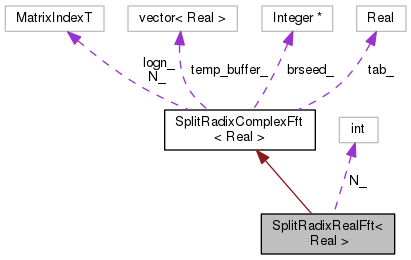
 Private Member Functions inherited from SplitRadixComplexFft< Real >
Private Member Functions inherited from SplitRadixComplexFft< Real > Private Attributes inherited from SplitRadixComplexFft< Real >
Private Attributes inherited from SplitRadixComplexFft< Real > Private Types inherited from SplitRadixComplexFft< Real >
Private Types inherited from SplitRadixComplexFft< Real >