Functions
Matrix-vector functions returning scalars
%Matrix and vector classes
Collaboration diagram for Matrix-vector functions returning scalars:

Functions

template<typename Real >
bool ApproxEqual (const MatrixBase< Real > &A, const MatrixBase< Real > &B, Real tol=0.01)
 
template<typename Real >
void AssertEqual (const MatrixBase< Real > &A, const MatrixBase< Real > &B, float tol=0.01)
 
template<typename Real >
double TraceMat (const MatrixBase< Real > &A)
 Returns trace of matrix. More...
 
template<typename Real >
Real TraceMatMatMat (const MatrixBase< Real > &A, MatrixTransposeType transA, const MatrixBase< Real > &B, MatrixTransposeType transB, const MatrixBase< Real > &C, MatrixTransposeType transC)
 Returns tr(A B C) More...
 
template<typename Real >
Real TraceMatMatMatMat (const MatrixBase< Real > &A, MatrixTransposeType transA, const MatrixBase< Real > &B, MatrixTransposeType transB, const MatrixBase< Real > &C, MatrixTransposeType transC, const MatrixBase< Real > &D, MatrixTransposeType transD)
 Returns tr(A B C D) More...
 
template<typename Real >
bool ApproxEqual (const VectorBase< Real > &a, const VectorBase< Real > &b, Real tol=0.01)
 
template<typename Real >
void AssertEqual (VectorBase< Real > &a, VectorBase< Real > &b, float tol=0.01)
 
template<typename Real >
Real VecVec (const VectorBase< Real > &v1, const VectorBase< Real > &v2)
 Returns dot product between v1 and v2. More...
 
template<typename Real , typename OtherReal >
Real VecVec (const VectorBase< Real > &ra, const VectorBase< OtherReal > &rb)
 
template<typename Real >
Real VecMatVec (const VectorBase< Real > &v1, const MatrixBase< Real > &M, const VectorBase< Real > &v2)
 Returns 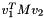$ v_1^T M v_2 $ . More...
 
float TraceSpSp (const SpMatrix< float > &A, const SpMatrix< float > &B)
 Returns tr(A B). More...
 
double TraceSpSp (const SpMatrix< double > &A, const SpMatrix< double > &B)
 
template<typename Real >
bool ApproxEqual (const SpMatrix< Real > &A, const SpMatrix< Real > &B, Real tol=0.01)
 
template<typename Real >
void AssertEqual (const SpMatrix< Real > &A, const SpMatrix< Real > &B, Real tol=0.01)
 
template<typename Real , typename OtherReal >
Real TraceSpSp (const SpMatrix< Real > &A, const SpMatrix< OtherReal > &B)
 Returns tr(A B). More...
 
template<typename Real >
Real TraceSpSpLower (const SpMatrix< Real > &A, const SpMatrix< Real > &B)
 
template<typename Real >
Real TraceSpMat (const SpMatrix< Real > &A, const MatrixBase< Real > &B)
 Returns tr(A B). More...
 
template<typename Real >
Real TraceMatSpMat (const MatrixBase< Real > &A, MatrixTransposeType transA, const SpMatrix< Real > &B, const MatrixBase< Real > &C, MatrixTransposeType transC)
 Returns tr(A B C) (A and C may be transposed as specified by transA and transC). More...
 
template<typename Real >
Real TraceMatSpMatSp (const MatrixBase< Real > &A, MatrixTransposeType transA, const SpMatrix< Real > &B, const MatrixBase< Real > &C, MatrixTransposeType transC, const SpMatrix< Real > &D)
 Returns tr (A B C D) (A and C may be transposed as specified by transA and transB). More...
 
template<typename Real >
Real VecSpVec (const VectorBase< Real > &v1, const SpMatrix< Real > &M, const VectorBase< Real > &v2)
 Computes v1^T * M * v2. More...
 

Detailed Description

Function Documentation

◆ ApproxEqual() [1/3]

bool kaldi::ApproxEqual ( const SpMatrix< Real > &  A,
const SpMatrix< Real > &  B,
Real  tol = 0.01 
)
inline

Definition at line 375 of file sp-matrix.h.

376  {
377  return A.ApproxEqual(B, tol);
378 }

◆ ApproxEqual() [2/3]

bool kaldi::ApproxEqual ( const VectorBase< Real > &  a,
const VectorBase< Real > &  b,
Real  tol = 0.01 
)

Definition at line 576 of file kaldi-vector.h.

References VectorBase< Real >::ApproxEqual().

577  {
578  return a.ApproxEqual(b, tol);
579 }

◆ ApproxEqual() [3/3]

bool kaldi::ApproxEqual ( const MatrixBase< Real > &  A,
const MatrixBase< Real > &  B,
Real  tol = 0.01 
)

Definition at line 1029 of file kaldi-matrix.h.

References MatrixBase< Real >::ApproxEqual().

1030  {
1031  return A.ApproxEqual(B, tol);
1032 }

◆ AssertEqual() [1/3]

void kaldi::AssertEqual ( const SpMatrix< Real > &  A,
const SpMatrix< Real > &  B,
Real  tol = 0.01 
)
inline

Definition at line 381 of file sp-matrix.h.

References SpMatrix< Real >::ApproxEqual(), KALDI_ASSERT, kaldi::TraceMatSpMat(), kaldi::TraceMatSpMatSp(), kaldi::TraceSpMat(), kaldi::TraceSpSp(), kaldi::TraceSpSpLower(), and kaldi::VecSpVec().

382  {
383  KALDI_ASSERT(ApproxEqual(A, B, tol));
384 }
kaldi::ApproxEqual
bool ApproxEqual(const SpMatrix< Real > &A, const SpMatrix< Real > &B, Real tol=0.01)
Definition: sp-matrix.h:375
KALDI_ASSERT
#define KALDI_ASSERT(cond)
Definition: kaldi-error.h:185

◆ AssertEqual() [2/3]

void kaldi::AssertEqual ( VectorBase< Real > &  a,
VectorBase< Real > &  b,
float  tol = 0.01 
)
inline

Definition at line 582 of file kaldi-vector.h.

References VectorBase< Real >::ApproxEqual(), KALDI_ASSERT, kaldi::VecMatVec(), and kaldi::VecVec().

583  {
584  KALDI_ASSERT(a.ApproxEqual(b, tol));
585 }
KALDI_ASSERT
#define KALDI_ASSERT(cond)
Definition: kaldi-error.h:185

◆ AssertEqual() [3/3]

void kaldi::AssertEqual ( const MatrixBase< Real > &  A,
const MatrixBase< Real > &  B,
float  tol = 0.01 
)
inline

Definition at line 1035 of file kaldi-matrix.h.

References MatrixBase< Real >::ApproxEqual(), and KALDI_ASSERT.

1036  {
1037  KALDI_ASSERT(A.ApproxEqual(B, tol));
1038 }
KALDI_ASSERT
#define KALDI_ASSERT(cond)
Definition: kaldi-error.h:185

◆ TraceMat()

double kaldi::TraceMat ( const MatrixBase< Real > &  A)

Returns trace of matrix.

Definition at line 1042 of file kaldi-matrix.h.

References kaldi::AttemptComplexPower(), kaldi::CreateEigenvalueMatrix(), kaldi::operator>>(), kaldi::SortSvd(), MatrixBase< Real >::Trace(), kaldi::TraceMatMatMat(), and kaldi::TraceMatMatMatMat().

Referenced by kaldi::CalBasisFmllrStepSize(), kaldi::CalcFmllrStepSize(), and kaldi::UnitTestTrace().

1042 { return A.Trace(); }

◆ TraceMatMatMat()

Real TraceMatMatMat ( const MatrixBase< Real > &  A,
MatrixTransposeType  transA,
const MatrixBase< Real > &  B,
MatrixTransposeType  transB,
const MatrixBase< Real > &  C,
MatrixTransposeType  transC 
)

Returns tr(A B C)

Definition at line 2502 of file kaldi-matrix.cc.

References MatrixBase< Real >::AddMatMat(), KALDI_ASSERT, kaldi::kTrans, MatrixBase< Real >::NumCols(), MatrixBase< Real >::NumRows(), kaldi::swap(), kaldi::TraceMatMat(), and kaldi::TraceMatMatMat().

Referenced by kaldi::TraceMat(), and kaldi::UnitTestTrace().

2504  {
2505  MatrixIndexT ARows = A.NumRows(), ACols = A.NumCols(), BRows = B.NumRows(), BCols = B.NumCols(),
2506  CRows = C.NumRows(), CCols = C.NumCols();
2507  if (transA == kTrans) std::swap(ARows, ACols);
2508  if (transB == kTrans) std::swap(BRows, BCols);
2509  if (transC == kTrans) std::swap(CRows, CCols);
2510  KALDI_ASSERT( CCols == ARows && ACols == BRows && BCols == CRows && "TraceMatMatMat: args have mismatched dimensions.");
2511  if (ARows*BCols < std::min(BRows*CCols, CRows*ACols)) {
2512  Matrix<Real> AB(ARows, BCols);
2513  AB.AddMatMat(1.0, A, transA, B, transB, 0.0); // AB = A * B.
2514  return TraceMatMat(AB, C, transC);
2515  } else if ( BRows*CCols < CRows*ACols) {
2516  Matrix<Real> BC(BRows, CCols);
2517  BC.AddMatMat(1.0, B, transB, C, transC, 0.0); // BC = B * C.
2518  return TraceMatMat(BC, A, transA);
2519  } else {
2520  Matrix<Real> CA(CRows, ACols);
2521  CA.AddMatMat(1.0, C, transC, A, transA, 0.0); // CA = C * A
2522  return TraceMatMat(CA, B, transB);
2523  }
2524 }
kaldi::TraceMatMat
template double TraceMatMat(const MatrixBase< double > &A, const MatrixBase< double > &B, MatrixTransposeType trans)
kaldi::swap
void swap(basic_filebuf< CharT, Traits > &x, basic_filebuf< CharT, Traits > &y)
Definition: basic-filebuf.h:275
kaldi::MatrixIndexT
int32 MatrixIndexT
Definition: matrix-common.h:98
KALDI_ASSERT
#define KALDI_ASSERT(cond)
Definition: kaldi-error.h:185

◆ TraceMatMatMatMat()

Real TraceMatMatMatMat ( const MatrixBase< Real > &  A,
MatrixTransposeType  transA,
const MatrixBase< Real > &  B,
MatrixTransposeType  transB,
const MatrixBase< Real > &  C,
MatrixTransposeType  transC,
const MatrixBase< Real > &  D,
MatrixTransposeType  transD 
)

Returns tr(A B C D)

Definition at line 2538 of file kaldi-matrix.cc.

References MatrixBase< Real >::AddMatMat(), KALDI_ASSERT, kaldi::kNoTrans, kaldi::kTrans, MatrixBase< Real >::NumCols(), MatrixBase< Real >::NumRows(), kaldi::swap(), kaldi::TraceMatMatMat(), and kaldi::TraceMatMatMatMat().

Referenced by kaldi::TraceMat(), and kaldi::UnitTestTrace().

2541  {
2542  MatrixIndexT ARows = A.NumRows(), ACols = A.NumCols(), BRows = B.NumRows(), BCols = B.NumCols(),
2543  CRows = C.NumRows(), CCols = C.NumCols(), DRows = D.NumRows(), DCols = D.NumCols();
2544  if (transA == kTrans) std::swap(ARows, ACols);
2545  if (transB == kTrans) std::swap(BRows, BCols);
2546  if (transC == kTrans) std::swap(CRows, CCols);
2547  if (transD == kTrans) std::swap(DRows, DCols);
2548  KALDI_ASSERT( DCols == ARows && ACols == BRows && BCols == CRows && CCols == DRows && "TraceMatMatMat: args have mismatched dimensions.");
2549  if (ARows*BCols < std::min(BRows*CCols, std::min(CRows*DCols, DRows*ACols))) {
2550  Matrix<Real> AB(ARows, BCols);
2551  AB.AddMatMat(1.0, A, transA, B, transB, 0.0); // AB = A * B.
2552  return TraceMatMatMat(AB, kNoTrans, C, transC, D, transD);
2553  } else if ((BRows*CCols) < std::min(CRows*DCols, DRows*ACols)) {
2554  Matrix<Real> BC(BRows, CCols);
2555  BC.AddMatMat(1.0, B, transB, C, transC, 0.0); // BC = B * C.
2556  return TraceMatMatMat(BC, kNoTrans, D, transD, A, transA);
2557  } else if (CRows*DCols < DRows*ACols) {
2558  Matrix<Real> CD(CRows, DCols);
2559  CD.AddMatMat(1.0, C, transC, D, transD, 0.0); // CD = C * D
2560  return TraceMatMatMat(CD, kNoTrans, A, transA, B, transB);
2561  } else {
2562  Matrix<Real> DA(DRows, ACols);
2563  DA.AddMatMat(1.0, D, transD, A, transA, 0.0); // DA = D * A
2564  return TraceMatMatMat(DA, kNoTrans, B, transB, C, transC);
2565  }
2566 }
kaldi::swap
void swap(basic_filebuf< CharT, Traits > &x, basic_filebuf< CharT, Traits > &y)
Definition: basic-filebuf.h:275
kaldi::TraceMatMatMat
template double TraceMatMatMat(const MatrixBase< double > &A, MatrixTransposeType transA, const MatrixBase< double > &B, MatrixTransposeType transB, const MatrixBase< double > &C, MatrixTransposeType transC)
kaldi::MatrixIndexT
int32 MatrixIndexT
Definition: matrix-common.h:98
KALDI_ASSERT
#define KALDI_ASSERT(cond)
Definition: kaldi-error.h:185

◆ TraceMatSpMat()

Real TraceMatSpMat ( const MatrixBase< Real > &  A,
MatrixTransposeType  transA,
const SpMatrix< Real > &  B,
const MatrixBase< Real > &  C,
MatrixTransposeType  transC 
)

Returns tr(A B C) (A and C may be transposed as specified by transA and transC).

Definition at line 415 of file sp-matrix.cc.

References MatrixBase< Real >::AddMatMat(), KALDI_ASSERT, kaldi::kTrans, MatrixBase< Real >::NumCols(), MatrixBase< Real >::NumRows(), PackedMatrix< Real >::NumRows(), and kaldi::TraceSpMat().

Referenced by kaldi::AssertEqual(), kaldi::UnitTestSolve(), and kaldi::UnitTestTrace().

417  {
418  KALDI_ASSERT((transA == kTrans?A.NumCols():A.NumRows()) ==
419  (transC == kTrans?C.NumRows():C.NumCols()) &&
420  (transA == kTrans?A.NumRows():A.NumCols()) == B.NumRows() &&
421  (transC == kTrans?C.NumCols():C.NumRows()) == B.NumRows() &&
422  "TraceMatSpMat: arguments have wrong dimension.");
423  Matrix<Real> tmp(B.NumRows(), B.NumRows());
424  tmp.AddMatMat(1.0, C, transC, A, transA, 0.0); // tmp = C * A.
425  return TraceSpMat(B, tmp);
426 }
kaldi::TraceSpMat
template double TraceSpMat(const SpMatrix< double > &A, const MatrixBase< double > &B)
KALDI_ASSERT
#define KALDI_ASSERT(cond)
Definition: kaldi-error.h:185

◆ TraceMatSpMatSp()

Real TraceMatSpMatSp ( const MatrixBase< Real > &  A,
MatrixTransposeType  transA,
const SpMatrix< Real > &  B,
const MatrixBase< Real > &  C,
MatrixTransposeType  transC,
const SpMatrix< Real > &  D 
)

Returns tr (A B C D) (A and C may be transposed as specified by transA and transB).

Definition at line 438 of file sp-matrix.cc.

References MatrixBase< Real >::AddMatSp(), KALDI_ASSERT, kaldi::kNoTrans, kaldi::kTrans, MatrixBase< Real >::NumCols(), PackedMatrix< Real >::NumCols(), MatrixBase< Real >::NumRows(), PackedMatrix< Real >::NumRows(), and kaldi::TraceMatMat().

Referenced by kaldi::AssertEqual(), kaldi::CalcFmllrStepSize(), kaldi::UnitTestSolve(), and kaldi::UnitTestTrace().

440  {
441  KALDI_ASSERT((transA == kTrans ?A.NumCols():A.NumRows() == D.NumCols()) &&
442  (transA == kTrans ? A.NumRows():A.NumCols() == B.NumRows()) &&
443  (transC == kTrans ? A.NumCols():A.NumRows() == B.NumCols()) &&
444  (transC == kTrans ? A.NumRows():A.NumCols() == D.NumRows()) &&
445  "KALDI_ERR: TraceMatSpMatSp: arguments have mismatched dimension.");
446  // Could perhaps optimize this more depending on dimensions of quantities.
447  Matrix<Real> tmpAB(transA == kTrans ? A.NumCols():A.NumRows(), B.NumCols());
448  tmpAB.AddMatSp(1.0, A, transA, B, 0.0);
449  Matrix<Real> tmpCD(transC == kTrans ? C.NumCols():C.NumRows(), D.NumCols());
450  tmpCD.AddMatSp(1.0, C, transC, D, 0.0);
451  return TraceMatMat(tmpAB, tmpCD, kNoTrans);
452 }
kaldi::TraceMatMat
Real TraceMatMat(const MatrixBase< Real > &A, const MatrixBase< Real > &B, MatrixTransposeType trans)
We need to declare this here as it will be a friend function.
Definition: kaldi-matrix.cc:2692
KALDI_ASSERT
#define KALDI_ASSERT(cond)
Definition: kaldi-error.h:185

◆ TraceSpMat()

Real TraceSpMat ( const SpMatrix< Real > &  A,
const MatrixBase< Real > &  B 
)

Returns tr(A B).

No option to transpose B because would make no difference.

Definition at line 389 of file sp-matrix.cc.

References MatrixBase< Real >::Data(), PackedMatrix< Real >::Data(), KALDI_ASSERT, MatrixBase< Real >::NumCols(), PackedMatrix< Real >::NumCols(), MatrixBase< Real >::NumRows(), PackedMatrix< Real >::NumRows(), and MatrixBase< Real >::Stride().

Referenced by kaldi::AssertEqual(), kaldi::TraceMatSpMat(), and kaldi::UnitTestTrace().

389  {
390  KALDI_ASSERT(A.NumRows() == B.NumRows() && A.NumCols() == B.NumCols() &&
391  "KALDI_ERR: TraceSpMat: arguments have mismatched dimension");
392  MatrixIndexT R = A.NumRows();
393  Real ans = (Real)0.0;
394  const Real *Aptr = A.Data(), *Bptr = B.Data();
395  MatrixIndexT bStride = B.Stride();
396  for (MatrixIndexT r = 0;r < R;r++) {
397  for (MatrixIndexT c = 0;c < r;c++) {
398  // ans += A(r, c) * (B(r, c) + B(c, r));
399  ans += *(Aptr++) * (Bptr[r*bStride + c] + Bptr[c*bStride + r]);
400  }
401  // ans += A(r, r) * B(r, r);
402  ans += *(Aptr++) * Bptr[r*bStride + r];
403  }
404  return ans;
405 }
kaldi::MatrixIndexT
int32 MatrixIndexT
Definition: matrix-common.h:98
KALDI_ASSERT
#define KALDI_ASSERT(cond)
Definition: kaldi-error.h:185

◆ TraceSpSp() [1/3]

double TraceSpSp ( const SpMatrix< double > &  A,
const SpMatrix< double > &  B 
)

Definition at line 326 of file sp-matrix.cc.

References kaldi::cblas_Xdot(), PackedMatrix< Real >::Data(), KALDI_ASSERT, and PackedMatrix< Real >::NumRows().

Referenced by kaldi::AssertEqual(), MleAmSgmm2Updater::ComputeMPrior(), PldaEstimator::ComputeObjfPart1(), IvectorExtractor::GetAcousticAuxfMean(), IvectorExtractor::GetAcousticAuxfVariance(), IvectorExtractor::GetAcousticAuxfWeight(), CuSpMatrix< Real >::IsUnit(), SpMatrix< float >::LimitCondDouble(), kaldi::MlObjective(), kaldi::SolveQuadraticMatrixProblem(), kaldi::TraceSpSp(), kaldi::UnitTestCuSpMatrixTraceSpSp(), kaldi::UnitTestDeterminant(), kaldi::UnitTestTraceSpSpLower(), IvectorExtractorStats::UpdateVariances(), EbwAmSgmm2Updater::UpdateVars(), and MleAmSgmm2Updater::UpdateVars().

326  {
327  KALDI_ASSERT(A.NumRows() == B.NumRows());
328  const double *Aptr = A.Data();
329  const double *Bptr = B.Data();
330  MatrixIndexT R = A.NumRows();
331  MatrixIndexT RR = (R * (R + 1)) / 2;
332  double all_twice = 2.0 * cblas_Xdot(RR, Aptr, 1, Bptr, 1);
333  // "all_twice" contains twice the vector-wise dot-product... this is
334  // what we want except the diagonal elements are represented
335  // twice.
336  double diag_once = 0.0;
337  for (MatrixIndexT row_plus_two = 2; row_plus_two <= R + 1; row_plus_two++) {
338  diag_once += *Aptr * *Bptr;
339  Aptr += row_plus_two;
340  Bptr += row_plus_two;
341  }
342  return all_twice - diag_once;
343 }
kaldi::PackedMatrix::NumRows
MatrixIndexT NumRows() const
Definition: packed-matrix.h:104
kaldi::cblas_Xdot
float cblas_Xdot(const int N, const float *const X, const int incX, const float *const Y, const int incY)
Definition: cblas-wrappers.h:64
kaldi::MatrixIndexT
int32 MatrixIndexT
Definition: matrix-common.h:98
KALDI_ASSERT
#define KALDI_ASSERT(cond)
Definition: kaldi-error.h:185

◆ TraceSpSp() [2/3]

float TraceSpSp ( const SpMatrix< float > &  A,
const SpMatrix< float > &  B 
)

Returns tr(A B).

Definition at line 346 of file sp-matrix.cc.

References kaldi::cblas_Xdot(), PackedMatrix< Real >::Data(), KALDI_ASSERT, and PackedMatrix< Real >::NumRows().

346  {
347  KALDI_ASSERT(A.NumRows() == B.NumRows());
348  const float *Aptr = A.Data();
349  const float *Bptr = B.Data();
350  MatrixIndexT R = A.NumRows();
351  MatrixIndexT RR = (R * (R + 1)) / 2;
352  float all_twice = 2.0 * cblas_Xdot(RR, Aptr, 1, Bptr, 1);
353  // "all_twice" contains twice the vector-wise dot-product... this is
354  // what we want except the diagonal elements are represented
355  // twice.
356  float diag_once = 0.0;
357  for (MatrixIndexT row_plus_two = 2; row_plus_two <= R + 1; row_plus_two++) {
358  diag_once += *Aptr * *Bptr;
359  Aptr += row_plus_two;
360  Bptr += row_plus_two;
361  }
362  return all_twice - diag_once;
363 }
kaldi::PackedMatrix::NumRows
MatrixIndexT NumRows() const
Definition: packed-matrix.h:104
kaldi::cblas_Xdot
float cblas_Xdot(const int N, const float *const X, const int incX, const float *const Y, const int incY)
Definition: cblas-wrappers.h:64
kaldi::MatrixIndexT
int32 MatrixIndexT
Definition: matrix-common.h:98
KALDI_ASSERT
#define KALDI_ASSERT(cond)
Definition: kaldi-error.h:185

◆ TraceSpSp() [3/3]

Real TraceSpSp ( const SpMatrix< Real > &  A,
const SpMatrix< OtherReal > &  B 
)

Returns tr(A B).

Definition at line 367 of file sp-matrix.cc.

References PackedMatrix< Real >::Data(), KALDI_ASSERT, PackedMatrix< Real >::NumRows(), kaldi::TraceSpSp< double, float >(), and kaldi::TraceSpSp< float, double >().

367  {
368  KALDI_ASSERT(A.NumRows() == B.NumRows());
369  Real ans = 0.0;
370  const Real *Aptr = A.Data();
371  const OtherReal *Bptr = B.Data();
372  MatrixIndexT row, col, R = A.NumRows();
373  for (row = 0; row < R; row++) {
374  for (col = 0; col < row; col++)
375  ans += 2.0 * *(Aptr++) * *(Bptr++);
376  ans += *(Aptr++) * *(Bptr++); // Diagonal.
377  }
378  return ans;
379 }
kaldi::MatrixIndexT
int32 MatrixIndexT
Definition: matrix-common.h:98
KALDI_ASSERT
#define KALDI_ASSERT(cond)
Definition: kaldi-error.h:185

◆ TraceSpSpLower()

Real TraceSpSpLower ( const SpMatrix< Real > &  A,
const SpMatrix< Real > &  B 
)

Definition at line 1171 of file sp-matrix.cc.

References kaldi::cblas_Xdot(), PackedMatrix< Real >::Data(), KALDI_ASSERT, PackedMatrix< Real >::NumRows(), kaldi::SolveDoubleQuadraticMatrixProblem(), and kaldi::SolveQuadraticMatrixProblem().

Referenced by kaldi::AssertEqual(), FullGmm::LogLikelihoods(), FullGmm::LogLikelihoodsPreselect(), and kaldi::UnitTestTraceSpSpLower().

1171  {
1172  MatrixIndexT adim = A.NumRows();
1173  KALDI_ASSERT(adim == B.NumRows());
1174  MatrixIndexT dim = (adim*(adim+1))/2;
1175  return cblas_Xdot(dim, A.Data(), 1, B.Data(), 1);
1176 }
kaldi::cblas_Xdot
float cblas_Xdot(const int N, const float *const X, const int incX, const float *const Y, const int incY)
Definition: cblas-wrappers.h:64
kaldi::MatrixIndexT
int32 MatrixIndexT
Definition: matrix-common.h:98
KALDI_ASSERT
#define KALDI_ASSERT(cond)
Definition: kaldi-error.h:185

◆ VecMatVec()

Real VecMatVec ( const VectorBase< Real > &  v1,
const MatrixBase< Real > &  M,
const VectorBase< Real > &  v2 
)

Returns 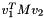$ v_1^T M v_2 $ .

Not as efficient as it could be where v1 == v2.

Definition at line 1281 of file kaldi-vector.cc.

References VectorBase< Real >::AddMatVec(), VectorBase< Real >::Dim(), KALDI_ASSERT, kaldi::kNoTrans, MatrixBase< Real >::NumCols(), MatrixBase< Real >::NumRows(), kaldi::VecMatVec(), and kaldi::VecVec().

Referenced by kaldi::AssertEqual(), kaldi::UnitTestVecMatVec(), kaldi::VecMatVec(), and Vector< float >::Vector().

1282  {
1283  KALDI_ASSERT(v1.Dim() == M.NumRows() && v2.Dim() == M.NumCols());
1284  Vector<Real> vtmp(M.NumRows());
1285  vtmp.AddMatVec(1.0, M, kNoTrans, v2, 0.0);
1286  return VecVec(v1, vtmp);
1287 }
kaldi::VecVec
template double VecVec(const VectorBase< double > &ra, const VectorBase< float > &rb)
KALDI_ASSERT
#define KALDI_ASSERT(cond)
Definition: kaldi-error.h:185

◆ VecSpVec()

Real VecSpVec ( const VectorBase< Real > &  v1,
const SpMatrix< Real > &  M,
const VectorBase< Real > &  v2 
)

Computes v1^T * M * v2.

Not as efficient as it could be where v1 == v2 (but no suitable blas routines available).Returns 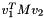$ v_1^T M v_2 $ Not as efficient as it could be where v1 == v2.

Definition at line 964 of file sp-matrix.cc.

References kaldi::cblas_Xspmv(), VectorBase< Real >::Data(), PackedMatrix< Real >::Data(), VectorBase< Real >::Dim(), KALDI_ASSERT, PackedMatrix< Real >::NumRows(), and kaldi::VecVec().

Referenced by kaldi::AssertEqual(), FullGmm::ComponentLogLikelihood(), FullGmm::ComputeGconsts(), PldaEstimator::ComputeObjfPart2(), IvectorExtractor::GetAcousticAuxfMean(), FmllrRawAccs::GetAuxf(), GetLogLikeTest(), main(), OnlineIvectorEstimationStats::Objf(), kaldi::SolveDoubleQuadraticMatrixProblem(), kaldi::SolveQuadraticProblem(), kaldi::UnitTestFloorChol(), UnitTestFullGmm(), kaldi::UnitTestInnerProd(), kaldi::UnitTestLbfgs(), kaldi::UnitTestSolve(), MlltAccs::Update(), MleAmSgmm2Updater::UpdatePhoneVectorsInternal(), MleAmSgmm2Updater::UpdateW(), and MleSgmm2SpeakerAccs::UpdateWithU().

965  {
966  MatrixIndexT D = M.NumRows();
967  KALDI_ASSERT(v1.Dim() == D && v1.Dim() == v2.Dim());
968  Vector<Real> tmp_vec(D);
969  cblas_Xspmv(D, 1.0, M.Data(), v1.Data(), 1, 0.0, tmp_vec.Data(), 1);
970  return VecVec(tmp_vec, v2);
971 }
kaldi::MatrixIndexT
int32 MatrixIndexT
Definition: matrix-common.h:98
KALDI_ASSERT
#define KALDI_ASSERT(cond)
Definition: kaldi-error.h:185
kaldi::cblas_Xspmv
void cblas_Xspmv(const float alpha, const int num_rows, const float *Mdata, const float *v, const int v_inc, const float beta, float *y, const int y_inc)
Definition: cblas-wrappers.h:90
kaldi::VecVec
Real VecVec(const VectorBase< Real > &a, const VectorBase< Real > &b)
Returns dot product between v1 and v2.
Definition: kaldi-vector.cc:37

◆ VecVec() [1/2]

Real VecVec ( const VectorBase< Real > &  a,
const VectorBase< Real > &  b 
)

Returns dot product between v1 and v2.

Definition at line 37 of file kaldi-vector.cc.

References kaldi::cblas_Xdot(), VectorBase< Real >::Data(), VectorBase< Real >::Dim(), and KALDI_ASSERT.

Referenced by OptimizeLbfgs< Real >::AcceptStep(), OnlinePitchFeatureImpl::AcceptWaveform(), FmllrRawAccs::AccumulateForGmm(), kaldi::AddNoise(), kaldi::AssertEqual(), kaldi::CalBasisFmllrStepSize(), FullGmm::ComponentLogLikelihood(), DiagGmm::ComponentLogLikelihood(), SpectrogramComputer::Compute(), MelBanks::Compute(), MfccComputer::Compute(), FbankComputer::Compute(), PlpComputer::Compute(), kaldi::ComputeCorrelation(), kaldi::ComputeEarlyReverbEnergy(), OptimizeLbfgs< Real >::ComputeHifNeeded(), OptimizeLbfgs< Real >::ComputeNewDirection(), AmSgmm2::ComputeNormalizersInternal(), AmSgmm2::ComputePerFrameVars(), EbwAmSgmm2Updater::ComputePhoneVecStats(), LstmNonlinearityComponent::ConsolidateMemory(), kaldi::CuVectorUnitTestInvertElements(), kaldi::CuVectorUnitTestSum(), kaldi::CuVectorUnitTestVecVec(), ConvolutionComponent::DotProduct(), TimeHeightConvolutionComponent::DotProduct(), TdnnComponent::DotProduct(), RepeatedAffineComponent::DotProduct(), ConstantComponent::DotProduct(), AffineComponent::DotProduct(), BlockAffineComponent::DotProduct(), PerElementScaleComponent::DotProduct(), PerElementOffsetComponent::DotProduct(), ConstantFunctionComponent::DotProduct(), Convolutional1dComponent::DotProduct(), ScaleAndOffsetComponent::DotProduct(), kaldi::FindQuietestSegment(), kaldi::FmllrAuxfGradient(), kaldi::FmllrAuxFuncDiagGmm(), kaldi::FmllrInnerUpdate(), IvectorExtractor::GetAcousticAuxfGconst(), IvectorExtractor::GetAcousticAuxfMean(), IvectorExtractor::GetAcousticAuxfWeight(), FmllrRawAccs::GetAuxf(), Plda::GetNormalizationFactor(), IvectorExtractor::GetPriorAuxf(), AffineComponentPreconditioned::GetScalingFactor(), AffineComponent::Info(), AffineComponentPreconditioned::Info(), AffineComponentPreconditionedOnline::Info(), FixedAffineComponent::Info(), FixedScaleComponent::Info(), FixedBiasComponent::Info(), Convolutional1dComponent::Info(), kaldi::LinearCgd(), AmSgmm2::LogLikelihood(), Plda::LogLikelihoodRatio(), FullGmm::LogLikelihoodsPreselect(), DiagGmm::LogLikelihoodsPreselect(), DecodableAmDiagGmmRegtreeFmllr::LogLikelihoodZeroBased(), main(), kaldi::MllrAuxFunction(), kaldi::MlObjective(), VectorClusterable::Objf(), OnlineIvectorEstimationStats::Objf(), MatrixBase< float >::OrthogonalizeRows(), kaldi::nnet2::PreconditionDirections(), OnlineNaturalGradientSimple::PreconditionDirectionsCpu(), OnlinePreconditionerSimple::PreconditionDirectionsCpu(), kaldi::nnet3::PrintParameterStats(), kaldi::ProcessWindow(), ArbitraryResample::Resample(), LinearResample::Resample(), kaldi::SolveDoubleQuadraticMatrixProblem(), kaldi::SolveQuadraticProblem(), OptimizeLbfgs< Real >::StepSizeIteration(), kaldi::nnet3::SummarizeVector(), kaldi::TestCuVectorVecVecOne(), kaldi::nnet3::TestNnetComponentUpdatable(), SpMatrix< float >::TopEigs(), kaldi::TraceSpSp(), kaldi::UnitTestDotprod(), kaldi::UnitTestLbfgs(), UnitTestLinearResample2(), kaldi::UnitTestSnipEdges(), kaldi::UnitTestSolve(), kaldi::UnitTestSparseVectorVecSvec(), MlltAccs::Update(), MleAmSgmm2Updater::UpdatePhoneVectorsInternal(), OnlinePitchFeatureImpl::UpdateRemainder(), MleAmSgmm2Updater::UpdateW(), MleAmSgmm2Updater::UpdateWGetStats(), MleSgmm2SpeakerAccs::UpdateWithU(), kaldi::VecMatVec(), kaldi::VecSpVec(), VectorClusterable::VectorClusterable(), and kaldi::VecVec().

38  {
39  MatrixIndexT adim = a.Dim();
40  KALDI_ASSERT(adim == b.Dim());
41  return cblas_Xdot(adim, a.Data(), 1, b.Data(), 1);
42 }
kaldi::cblas_Xdot
float cblas_Xdot(const int N, const float *const X, const int incX, const float *const Y, const int incY)
Definition: cblas-wrappers.h:64
kaldi::MatrixIndexT
int32 MatrixIndexT
Definition: matrix-common.h:98
KALDI_ASSERT
#define KALDI_ASSERT(cond)
Definition: kaldi-error.h:185

◆ VecVec() [2/2]

Real VecVec ( const VectorBase< Real > &  ra,
const VectorBase< OtherReal > &  rb 
)

Definition at line 52 of file kaldi-vector.cc.

References VectorBase< Real >::Data(), VectorBase< Real >::Dim(), rnnlm::i, and KALDI_ASSERT.

53  {
54  MatrixIndexT adim = ra.Dim();
55  KALDI_ASSERT(adim == rb.Dim());
56  const Real *a_data = ra.Data();
57  const OtherReal *b_data = rb.Data();
58  Real sum = 0.0;
59  for (MatrixIndexT i = 0; i < adim; i++)
60  sum += a_data[i]*b_data[i];
61  return sum;
62 }
kaldi::MatrixIndexT
int32 MatrixIndexT
Definition: matrix-common.h:98
KALDI_ASSERT
#define KALDI_ASSERT(cond)
Definition: kaldi-error.h:185