BasisFmllrEstimate Class Reference

Estimation functions for basis fMLLR. More...

#include <basis-fmllr-diag-gmm.h>

Collaboration diagram for BasisFmllrEstimate:

Public Member Functions
	BasisFmllrEstimate ()
	BasisFmllrEstimate (int32 dim)
void	Write (std::ostream &out_stream, bool binary) const
	Routines for reading and writing fMLLR basis matrices. More...
void	Read (std::istream &in_stream, bool binary)
void	EstimateFmllrBasis (const AmDiagGmm &am_gmm, const BasisFmllrAccus &basis_accus)
	Estimate the base matrices efficiently in a Maximum Likelihood manner. More...
void	ComputeAmDiagPrecond (const AmDiagGmm &am_gmm, SpMatrix< double > *pre_cond)
	This function computes the preconditioner matrix, prior to base matrices estimation. More...
int32	Dim () const
int32	BasisSize () const
double	ComputeTransform (const AffineXformStats &spk_stats, Matrix< BaseFloat > *out_xform, Vector< BaseFloat > *coefficients, BasisFmllrOptions options) const
	This function performs speaker adaptation, computing the fMLLR matrix based on speaker statistics. More...

Private Attributes
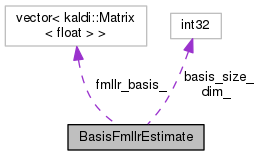
std::vector< Matrix< BaseFloat > >	fmllr_basis_
	Basis matrices. More...
int32	dim_
	Feature dimension. More...
int32	basis_size_
	Number of bases D*(D+1) More...

Detailed Description

Estimation functions for basis fMLLR.

Definition at line 107 of file basis-fmllr-diag-gmm.h.

Constructor & Destructor Documentation

BasisFmllrEstimate() [1/2]

BasisFmllrEstimate ( )

inline

Definition at line 110 of file basis-fmllr-diag-gmm.h.

: dim_(0), basis_size_(0) { }

BasisFmllrEstimate() [2/2]

BasisFmllrEstimate ( int32  dim )

inlineexplicit

Definition at line 111 of file basis-fmllr-diag-gmm.h.

                                         {
      dim_ = dim; basis_size_ = dim * (dim + 1);
  }

Member Function Documentation

BasisSize()

int32 BasisSize ( ) const

inline

Definition at line 139 of file basis-fmllr-diag-gmm.h.

{ return basis_size_; }

ComputeAmDiagPrecond()

void ComputeAmDiagPrecond	(	const AmDiagGmm &	am_gmm,
		SpMatrix< double > *	pre_cond
	)

This function computes the preconditioner matrix, prior to base matrices estimation.

Since the expected values of G statistics are used, it takes the acoustic model as the argument, rather than the actual accumulations AffineXformStats See section 5.1 of the paper.

Definition at line 156 of file basis-fmllr-diag-gmm.cc.

References VectorBase< Real >::AddVec2(), SpMatrix< Real >::CopyFromMat(), rnnlm::d, AmDiagGmm::Dim(), BasisFmllrAccus::dim_, DiagGmm::GetMeans(), AmDiagGmm::GetPdf(), DiagGmm::GetVars(), rnnlm::i, MatrixBase< Real >::IsSymmetric(), rnnlm::j, KALDI_ASSERT, KALDI_ERR, kaldi::kSetZero, kaldi::kTakeLower, DiagGmm::NumGauss(), AmDiagGmm::NumPdfs(), PackedMatrix< Real >::NumRows(), VectorBase< Real >::Range(), MatrixBase< Real >::Range(), SpMatrix< Real >::Resize(), MatrixBase< Real >::Row(), and DiagGmm::weights().

                                                                          {
  KALDI_ASSERT(am_gmm.Dim() == dim_);
  if (pre_cond->NumRows() != (dim_ + 1) * dim_)
    pre_cond->Resize((dim_ + 1) * dim_, kSetZero);

  int32 num_pdf = am_gmm.NumPdfs();
  Matrix<double> H_mat((dim_ + 1) * dim_, (dim_ + 1) * dim_);
  // expected values of fMLLR G statistics
  vector< SpMatrix<double> > G_hat(dim_);
  for (int32 d = 0; d < dim_; ++d)
       G_hat[d].Resize(dim_ + 1, kSetZero);

  // extend mean vectors with 1  [mule_jm 1]
  Vector<double> extend_mean(dim_ + 1);
  // extend covariance matrix with a row and column of 0
  Vector<double> extend_var(dim_ + 1);
  for (int32 j = 0; j < num_pdf; ++j) {
    const DiagGmm &diag_gmm = am_gmm.GetPdf(j);
    int32 num_comp = diag_gmm.NumGauss();
    // means, covariance and mixture weights for this diagonal GMM
    Matrix<double> means(num_comp, dim_);
    Matrix<double> vars(num_comp, dim_);
    diag_gmm.GetMeans(&means); diag_gmm.GetVars(&vars);
    Vector<BaseFloat> weights(diag_gmm.weights());

    for (int32 m = 0; m < num_comp; ++m) {
      extend_mean.Range(0, dim_).CopyFromVec(means.Row(m));
      extend_mean(dim_) = 1.0;
      extend_var.Range(0, dim_).CopyFromVec(vars.Row(m));
      extend_var(dim_) = 0;
      // loop over feature dimension
      // Eq. (28): G_hat {d} = \sum_{j, m} P_{j}{m} Inv_Sigma{j, m, d}
      // (mule_extend mule_extend^T + Sigma_extend)
      // where P_{j}{m} = P_{j} c_{j}{m}
      for (int32 d = 0; d < dim_; ++d) {
        double alpha = (1.0 / num_pdf) * weights(m) * (1.0 / vars.Row(m)(d));
        G_hat[d].AddVec2(alpha, extend_mean);
        // add vector to the diagonal elements of the matrix
        // not work for full covariance matrices
        G_hat[d].AddDiagVec(alpha, extend_var);
      } // loop over dimension
    } //  loop over Gaussians
  }  // loop over states

  // fill H_ with G_hat[i]; build the block diagonal structure
  // Eq. (31)
  for (int32 d = 0; d < dim_; d++) {
    H_mat.Range(d * (dim_ + 1), (dim_ + 1), d * (dim_ + 1), (dim_ + 1))
              .CopyFromSp(G_hat[d]);
  }

  // add the extra H(1) elements
  // Eq. (30) and Footnote 1 (0-based index)
  for (int32 i = 0; i < dim_; ++i)
    for (int32 j = 0; j < dim_; ++j)
      H_mat(i * (dim_ + 1) + j, j * (dim_ + 1) + i) += 1;
  // the final H should be symmetric
  if (!H_mat.IsSymmetric())
    KALDI_ERR << "Preconditioner matrix H = H(1) + H(2) is not symmetric";
  pre_cond->CopyFromMat(H_mat, kTakeLower);
}

ComputeTransform()

double ComputeTransform	(	const AffineXformStats &	spk_stats,
		Matrix< BaseFloat > *	out_xform,
		Vector< BaseFloat > *	coefficients,
		BasisFmllrOptions	options
	)		const

This function performs speaker adaptation, computing the fMLLR matrix based on speaker statistics.

It takes fMLLR stats as argument. The basis weights (d_{1}, d_{2}, ..., d_{N}) are also optimized explicitly. Finally, it returns objective function improvement over all the iterations, compared with the value at the initial value of "out_xform" (or the unit transform if not provided). The coefficients are output to "coefficients" only if the vector is provided. See section 5.3 of the paper for more details.

Definition at line 270 of file basis-fmllr-diag-gmm.cc.

References MatrixBase< Real >::AddMat(), VectorBase< Real >::AddVec(), AffineXformStats::beta_, kaldi::CalBasisFmllrStepSize(), MatrixBase< Real >::CopyFromMat(), rnnlm::d, AffineXformStats::dim_, BasisFmllrAccus::dim_, kaldi::FmllrAuxFuncDiagGmm(), AffineXformStats::G_, MatrixBase< Real >::InvertDouble(), MatrixBase< Real >::IsZero(), AffineXformStats::K_, KALDI_ASSERT, KALDI_VLOG, KALDI_WARN, kaldi::kNoTrans, kaldi::kSetZero, kaldi::kTrans, BasisFmllrOptions::min_count, rnnlm::n, BasisFmllrOptions::num_iters, MatrixBase< Real >::NumCols(), MatrixBase< Real >::NumRows(), MatrixBase< Real >::Range(), Vector< Real >::Resize(), Matrix< Real >::Resize(), MatrixBase< Real >::Row(), MatrixBase< Real >::Scale(), MatrixBase< Real >::SetUnit(), MatrixBase< Real >::SetZero(), BasisFmllrOptions::size_scale, BasisFmllrOptions::step_size_iters, kaldi::TraceMatMat(), and Matrix< Real >::Transpose().

Referenced by SingleUtteranceGmmDecoder::EstimateFmllr(), and main().

                                     {
  if (coefficient == NULL) {
    Vector<BaseFloat> tmp;
    return ComputeTransform(spk_stats, out_xform, &tmp, options);
  }
  KALDI_ASSERT(dim_ == spk_stats.dim_);
  if (spk_stats.beta_ < options.min_count) {
    KALDI_WARN << "Not updating fMLLR since count is below min-count: "
               << spk_stats.beta_;
    coefficient->Resize(0);
    return 0.0;
  } else {
    if (out_xform->NumRows() != dim_ || out_xform->NumCols() != (dim_ +1)) {
      out_xform->Resize(dim_, dim_ + 1, kSetZero);
    }
    // Initialized either as [I;0] or as the current transform
    Matrix<BaseFloat> W_mat(dim_, dim_ + 1);
    if (out_xform->IsZero()) {
      W_mat.SetUnit();
    } else {
      W_mat.CopyFromMat(*out_xform);
    }

    // Create temporary K and G quantities. Add for efficiency,
    // avoid repetitions of converting the stats from double
    // precision to single precision
    Matrix<BaseFloat> stats_tmp_K(spk_stats.K_);
    std::vector<SpMatrix<BaseFloat> > stats_tmp_G(dim_);
    for (int32 d = 0; d < dim_; d++)
      stats_tmp_G[d] = SpMatrix<BaseFloat>(spk_stats.G_[d]);

    // Number of bases for this speaker, according to the available
    // adaptation data
    int32 basis_size = int32 (std::min( double(basis_size_),
                               options.size_scale * spk_stats.beta_));

    coefficient->Resize(basis_size, kSetZero);

    BaseFloat impr_spk = 0;
    for (int32 iter = 1; iter <= options.num_iters; ++iter) {
      // Auxf computation based on FmllrAuxFuncDiagGmm from fmllr-diag-gmm.cc
      BaseFloat start_obj = FmllrAuxFuncDiagGmm(W_mat, spk_stats);

      // Contribution of quadratic terms to derivative
      // Eq. (37)  s_{d} = G_{d} w_{d}
      Matrix<BaseFloat> S(dim_, dim_ + 1);
      for (int32 d = 0; d < dim_; ++d)
        S.Row(d).AddSpVec(1.0, stats_tmp_G[d], W_mat.Row(d), 0.0);


      // W_mat = [A; b]
      Matrix<BaseFloat> A(dim_, dim_);
      A.CopyFromMat(W_mat.Range(0, dim_, 0, dim_));
      Matrix<BaseFloat> A_inv(A);
      A_inv.InvertDouble();
      Matrix<BaseFloat> A_inv_trans(A_inv);
      A_inv_trans.Transpose();
      // Compute gradient of auxf w.r.t. W_mat
      // Eq. (38)  P = beta [A^{-T}; 0] + K - S
      Matrix<BaseFloat> P(dim_, dim_ + 1);
      P.SetZero();
      P.Range(0, dim_, 0, dim_).CopyFromMat(A_inv_trans);
      P.Scale(spk_stats.beta_);
      P.AddMat(1.0, stats_tmp_K);
      P.AddMat(-1.0, S);

      // Compute directional gradient restricted by bases. Here we only use
      // the simple gradient method, rather than conjugate gradient. Finding
      // the optimal transformation W_mat is equivalent to optimizing weights
      // d_{1,2,...,N}.
      // Eq. (39)  delta(W) = \sum_n tr(\fmllr_basis_{n}^T \P) \fmllr_basis_{n}
      // delta(d_{n}) = tr(\fmllr_basis_{n}^T \P)
      Matrix<BaseFloat> delta_W(dim_, dim_ + 1);
      Vector<BaseFloat> delta_d(basis_size);
      for (int32 n = 0; n < basis_size; ++n) {
        delta_d(n) = TraceMatMat(fmllr_basis_[n], P, kTrans);
        delta_W.AddMat(delta_d(n), fmllr_basis_[n]);
      }

      BaseFloat step_size = CalBasisFmllrStepSize(spk_stats, stats_tmp_K,
        stats_tmp_G, delta_W, A, S, options.step_size_iters);
      W_mat.AddMat(step_size, delta_W, kNoTrans);
      coefficient->AddVec(step_size, delta_d);
      // Check auxiliary function
      BaseFloat end_obj = FmllrAuxFuncDiagGmm(W_mat, spk_stats);

      KALDI_VLOG(4) << "Objective function (iter=" << iter << "): "
                    << start_obj / spk_stats.beta_  << " -> "
                    << (end_obj / spk_stats.beta_) << " over "
                    << spk_stats.beta_ << " frames";

      impr_spk += (end_obj - start_obj);
    }  // loop over iters

    out_xform->CopyFromMat(W_mat, kNoTrans);
    return impr_spk;
  }
}

Dim()

int32 Dim ( ) const

inline

Definition at line 137 of file basis-fmllr-diag-gmm.h.

Referenced by SingleUtteranceGmmDecoder::EstimateFmllr().

{ return dim_; }

EstimateFmllrBasis()

void EstimateFmllrBasis	(	const AmDiagGmm &	am_gmm,
		const BasisFmllrAccus &	basis_accus
	)

Estimate the base matrices efficiently in a Maximum Likelihood manner.

It takes diagonal GMM as argument, which will be used for preconditioner computation. The total number of bases is fixed to N = (dim + 1) * dim Note that SVD is performed in the normalized space. The base matrices are finally converted back to the unnormalized space.

The sum of the [per-frame] eigenvalues is roughly equal to the improvement of log-likelihood of the training data.

Definition at line 219 of file basis-fmllr-diag-gmm.cc.

References SpMatrix< Real >::AddMat2Sp(), VectorBase< Real >::AddMatVec(), BasisFmllrAccus::beta_, TpMatrix< Real >::Cholesky(), MatrixBase< Real >::CopyFromTp(), BasisFmllrAccus::dim_, BasisFmllrAccus::grad_scatter_, TpMatrix< Real >::InvertDouble(), KALDI_LOG, kaldi::kNoTrans, kaldi::kSetZero, kaldi::kTrans, rnnlm::n, MatrixBase< Real >::Row(), VectorBase< Real >::Scale(), kaldi::SortSvd(), SpMatrix< Real >::SymPosSemiDefEig(), and Matrix< Real >::Transpose().

Referenced by main().

                                                                  {
  // Compute the preconditioner
  SpMatrix<double> precond_mat((dim_ + 1) * dim_);
  ComputeAmDiagPrecond(am_gmm, &precond_mat);
  // H = C C^T
  TpMatrix<double> C((dim_+1) * dim_);
  C.Cholesky(precond_mat);
  TpMatrix<double> C_inv(C);
  C_inv.InvertDouble();
  // From TpMatrix to Matrix
  Matrix<double> C_inv_full((dim_ + 1) * dim_, (dim_ + 1) * dim_);
  C_inv_full.CopyFromTp(C_inv);

  // Convert to the preconditioned coordinates
  // Eq. (35)  M_hat = C^{-1} grad_scatter C^{-T}
  SpMatrix<double> M_hat((dim_ + 1) * dim_);
  {
    SpMatrix<double> grad_scatter_d(basis_accus.grad_scatter_);
    M_hat.AddMat2Sp(1.0, C_inv_full, kNoTrans, grad_scatter_d, 0.0);
  }
  Vector<double> Lvec((dim_ + 1) * dim_);
  Matrix<double> U((dim_ + 1) * dim_, (dim_ + 1) * dim_);
  // SVD of M_hat; sort eigenvalues from greatest to smallest
  M_hat.SymPosSemiDefEig(&Lvec, &U);
  SortSvd(&Lvec, &U);
  // After transpose, each row is one base
  U.Transpose();

  fmllr_basis_.resize(basis_size_);
  for (int32 n = 0; n < basis_size_; ++n) {
    fmllr_basis_[n].Resize(dim_, dim_ + 1, kSetZero);
    Vector<double> basis_vec((dim_ + 1) * dim_);
    // Convert eigenvectors back to unnormalized space
    basis_vec.AddMatVec(1.0, C_inv_full, kTrans, U.Row(n), 0.0);
    // Convert stacked vectors to matrix
    fmllr_basis_[n].CopyRowsFromVec(basis_vec);
  }
  // Output the eigenvalues of the gradient scatter matrix
  // The eigenvalues are divided by twice the number of frames
  // in the training data, to get the per-frame values.
  Vector<double> Lvec_scaled(Lvec);
  Lvec_scaled.Scale(1.0 / (2 * basis_accus.beta_));
  KALDI_LOG << "The [per-frame] eigenvalues sorted from largest to smallest: " << Lvec_scaled;
  KALDI_LOG << "Sum of the [per-frame] eigenvalues, that is"
          " the log-likelihood improvement, is " << Lvec_scaled.Sum();
}

Read()

void Read	(	std::istream &	in_stream,
		bool	binary
	)

Definition at line 133 of file basis-fmllr-diag-gmm.cc.

References BasisFmllrAccus::dim_, kaldi::ExpectToken(), KALDI_ASSERT, rnnlm::n, and kaldi::ReadBasicType().

                                                         {
  uint32 tmp_uint32;
  string token;

  ExpectToken(is, binary, "<BASISFMLLRPARAM>");

  ExpectToken(is, binary, "<NUMBASIS>");
  ReadBasicType(is, binary, &tmp_uint32);
  basis_size_ = static_cast<int32>(tmp_uint32);
  KALDI_ASSERT(basis_size_ > 0);
  ExpectToken(is, binary, "<BASIS>");
  fmllr_basis_.resize(basis_size_);
  for (int32 n = 0; n < basis_size_; ++n) {
    fmllr_basis_[n].Read(is, binary);
    if (n == 0)
      dim_ = fmllr_basis_[n].NumRows();
    else {
      KALDI_ASSERT(dim_ == fmllr_basis_[n].NumRows());
    }
  }
  ExpectToken(is, binary, "</BASISFMLLRPARAM>");
}

Write()

void Write	(	std::ostream &	out_stream,
		bool	binary
	)		const

Routines for reading and writing fMLLR basis matrices.

Definition at line 116 of file basis-fmllr-diag-gmm.cc.

References rnnlm::n, kaldi::WriteBasicType(), and kaldi::WriteToken().

                                                                {
  uint32 tmp_uint32;

  WriteToken(os, binary, "<BASISFMLLRPARAM>");

  WriteToken(os, binary, "<NUMBASIS>");
  tmp_uint32 = static_cast<uint32>(basis_size_);
  WriteBasicType(os, binary, tmp_uint32);
  if (fmllr_basis_.size() != 0) {
    WriteToken(os, binary, "<BASIS>");
    for (int32 n = 0; n < basis_size_; ++n) {
      fmllr_basis_[n].Write(os, binary);
    }
  }
  WriteToken(os, binary, "</BASISFMLLRPARAM>");
}

Member Data Documentation

basis_size_

int32 basis_size_

private

Number of bases D*(D+1)

Definition at line 163 of file basis-fmllr-diag-gmm.h.

dim_

int32 dim_

private

Feature dimension.

Definition at line 161 of file basis-fmllr-diag-gmm.h.

fmllr_basis_

std::vector< Matrix<BaseFloat> > fmllr_basis_

private

Basis matrices.

Dim is [T] [D] [D+1] T is the number of bases

Definition at line 159 of file basis-fmllr-diag-gmm.h.

---

The documentation for this class was generated from the following files:

• transform/basis-fmllr-diag-gmm.h
• transform/basis-fmllr-diag-gmm.cc