Feature and model-space transforms in Kaldi

Introduction

Kaldi code currently supports a number of feature and model-space transformations and projections. Feature-space transforms and projections are treated in a consistent way by the tools (they are essientially just matrices), and the following sections relate to the commonalities:

Transforms, projections and other feature operations that are typically not speaker specific include:

Global transforms that are typically applied in a speaker adaptive way are:

We next discuss regression class trees and transforms that use them:

Applying global linear or affine feature transforms

In the case of feature-space transforms and projections that are global, and not associated with classes (e.g. speech/silence or regression classes), we represent them as matrices. A linear transform or projection is represented as a matrix by which we will left-multiply a feature vector, so the transformed feature is 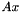$ A x $. An affine transform or projection is represented the same way, but we imagine a 1 has been appended to the feature vector, so the transformed feature is $ W \left[ \begin{array}{c} x \\ 1 \end{array} \right] $ where $ W = \left[ A ; b \right] $, with A and b being the linear transform and the constant offset. Note that this convention differs from some of the literature, where the 1 may appear as the first dimension rather than the last. Global transforms and projections are generally written as a type Matrix<BaseFloat> to a single file, and speaker or utterance-specific transforms or projections are stored in a table of such matrices (see The Table concept) indexed by speaker-id or utterance-id.

Transforms may be applied to features using the program transform-feats. Its syntax is 

 transform-feats <transform> <input-feats> <output-feats>

where <input-feats> is an rspecifier, <output-feats> is an wspecifier, and <transform> may be an rxfilename or an rspecifier (see Specifying Table formats: wspecifiers and rspecifiers and Extended filenames: rxfilenames and wxfilenames). The program will work out whether the transform is linear or affine based on whether or not the matrix's number of columns equals the feature dimension, or the feature dimension plus one. This program is typically used as part of a pipe. A typical example is: 

 feats="ark:splice-feats scp:data/train.scp ark:- |
          transform-feats $dir/0.mat ark:- ark:-|"
 some-program some-args "$feats" some-other-args ...

Here, the file 0.mat contains a single matrix. An example of applying speaker-specific transforms is: 

 feats="ark:add-deltas scp:data/train.scp ark:- |
   transform-feats --utt2spk=ark:data/train.utt2spk ark:$dir/0.trans ark:- ark:-|"
 some-program some-args "$feats" some-other-args ...

A per-utterance example would be as above but removing the –utt2spk option. In this example, the archive file 0.trans would contain transforms (e.g. CMLLR transforms) indexed by speaker-id, and the file data/train.utt2spk would have lines of the form "utt-id spk-id" (see next section for more explanation). The program transform-feats does not care how the transformation matrix was estimated, it just applies it to the features. After it has been through all the features it prints out the average per-frame log determinant. This can be useful when comparing objective functions (this log determinant would have to be added to the per-frame likelihood printed out by programs like gmm-align, gmm-acc-stats, or gmm-decode-kaldi). If the linear part A of the transformation (i.e. ignoring the offset term) is not square, then the program will instead print out the per-frame average of 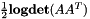$ \frac{1}{2} \mathbf{logdet} (A A^T) $. It refers to this as the pseudo-log-determinant. This is useful in checking convergence of MLLT estimation where the transformation matrix being applied is the MLLT matrix times an LDA matrix.

Speaker-independent versus per-speaker versus per-utterance adaptation

Programs that estimate transforms are generally set up to do a particular kind of adaptation, i.e. speaker-independent versus (speaker- or utterance-specific). For example, LDA and MLLT/STC transforms are speaker-independent but fMLLR transforms are speaker- or utterance-specific. Programs that estimate speaker- or utterance-specific transforms will work in per-utterance mode by default, but in per-speaker mode if the –spk2utt option is supplied (see below).

One program that can accept either speaker-independent or speaker- or utterance-specific transforms is transform-feats. This program detects whether the first argument (the transform) is an rxfilename (see Extended filenames: rxfilenames and wxfilenames) or an rspecifier (see Specifying Table formats: wspecifiers and rspecifiers). If the former, it treats it as a speaker-independent transform (e.g. a file containing a single matrix). If the latter, there are two choices. If no –utt2spk option is provided, it treats the transform as a table of matrices indexed by utterance id. If an –utt2spk option is provided (utt2spk is a table of strings indexed by utterance that contains the string-valued speaker id), then the transforms are assumed to be indexed by speaker id, and the table provided to the –utt2spk option is used to map each utterance to a speaker id.

Utterance-to-speaker and speaker-to-utterance maps

At this point we give a general overview of the –utt2spk and –spk2utt options. These options are accepted by programs that deal with transformations; they are used when you are doing per-speaker (as opposed to per-utterance) adaptation. Typically programs that process already-created transforms will need the –utt2spk option and programs that create the transforms will need the –spk2utt option. A typical case is that there will be a file called some-directory/utt2spk that looks like: 

spk1utt1  spk1
spk1utt2  spk1
spk2utt1  spk2
spk2utt2  spk2
...

where these strings are just examples, they stand for generic speaker and utterance identifiers; and there will be a file called some-directory/spk2utt that looks like: 

spk1 spk1utt1 spk1utt2
spk2 spk2utt1 spk2utt2
...

and you will supply options that look like –utt2spk=ark:some-directory/utt2spk or –spk2utt=ark:some-directory/spk2utt. The 'ark:' prefix is necessary because these files are given as rspecifiers by the Table code, and are interpreted as archives that contain strings (or vectors of strings, in the spk2utt case). Note that the utt2spk archive is generally accessed in a random-access manner, so if you are processing subsets of data it is safe to provide the whole file, but the spk2utt archive is accessed in a sequential manner so if you are using subsets of data you would have to split up the spk2utt archive.

Programs that accept the spk2utt option will normally iterate over the speaker-ids in the spk2utt file, and for each speaker-id they will iterate over the utterances for each speaker, accumulating statistics for each utterance. Access to the feature files will then be in random-access mode, rather than the normal sequential access. This requires some care to set up, because feature files are quite large and fully-processed features are normally read from an archive, which does not allow the most memory-efficient random access unless carefully set up. To avoid memory bloat when accessing the feature files in this case, it may be advisable to ensure that all archives are sorted on utterance-id, that the utterances in the file given to the –spk2utt option appear in sorted order, and that the appropriate options are given on the rspecifiers that specify the feature input to such programs (e.g. "ark,s,cs:-" if it is the standard input). See Avoiding memory bloat when reading archives in random-access mode for more discussion of this issue.

Composing transforms

Another program that accepts generic transforms is the program compose-transforms. The general syntax is "compose-transforms a b c", and it performs the multiplication c = a b (although this involves a little more than matrix multiplication if a is affine). An example modified from a script is as follows: 

 feats="ark:splice-feats scp:data/train.scp ark:- |
         transform-feats
           \"ark:compose-transforms ark:1.trans 0.mat ark:- |\"
           ark:- ark:- |"
 some-program some-args "$feats" ...

This example also illustrates using two levels of commands invoked from a program. Here, 0.mat is a global matrix (e.g. LDA) and 1.trans is a set of fMLLR/CMLLR matrices indexed by utterance id. The program compose-transforms composes the transforms together. The same features could be computed more simply, but less efficiently, as follows: 

 feats="ark:splice-feats scp:data/train.scp ark:- |
         transform-feats 0.mat ark:- ark:- |
         transform-feats ark:1.trans ark:- ark:- |"
 ...

In general, the transforms a and b that are the inputs to compose-transforms may be either speaker-independent transforms or speaker- or utterance-specific transforms. If a is utterance-specific and b is speaker-specific then you have to supply the –utt2spk option. However, the combination of a being speaker-specific and b being utterance-specific (which does not make much sense) is not supported. The output of compose-transforms will be a table if either a or b are tables. The three arguments a, b and c may all represent either tables or normal files (i.e. either {r,w}specifiers or {r,w}xfilenames), subject to consistency requirements.

If a is an affine transform, in order to perform the composition correctly, compose-transforms needs to know whether b is affine or linear (it does not know this because it does not have access to the dimension of the features that are transformed by b). This is controlled by the option –b-is-affine (bool, default false). If b is affine but you forget to set this option and a is affine, compose-transforms will treat b as a linear transform from dimension (the real input feature dimension) plus one, and will output a transform whose input dimension is (the real input feature dimension) plus two. There is no way for "transform-feats" to interpret this when it is to be applied to features, so the error should become obvious as a dimension mismatch at this point.

Silence weighting when estimating transforms

Eliminating silence frames can be helpful when estimating speaker adaptive transforms such as CMLLR. This even appears to be true when using a multi-class approach with a regression tree (for which, see Building regression trees for adaptation). The way we implement this is by weighting down the posteriors associated with silence phones. This takes place as a modification to the state-level posteriors. An extract of a bash shell script that does this is below (this script is discussed in more detail in Global CMLLR/fMLLR transforms): 

ali-to-post ark:$srcdir/test.ali ark:- | \
  weight-silence-post 0.0 $silphones $model ark:- ark:- | \
  gmm-est-fmllr --fmllr-min-count=$mincount \
    --spk2utt=ark:data/test.spk2utt $model "$sifeats" \
   ark,o:- ark:$dir/test.fmllr 2>$dir/fmllr.log

Here, the shell variable "silphones" would be set to a colon-separated list of the integer id's of the silence phones.

Linear Discriminant Analysis (LDA) transforms

Kaldi supports LDA estimation via class LdaEstimate. This class does not interact directly with any particular type of model; it needs to be initialized with the number of classes, and the accumulation function is declared as: 

class LdaEstimate {
  ...
  void Accumulate(const VectorBase<BaseFloat> &data, int32 class_id,
                  BaseFloat weight=1.0);
};

The program acc-lda accumulates LDA statistics using the acoustic states (i.e. pdf-ids) as the classes. It requires the transition model in order to map the alignments (expressed in terms of transition-ids) to pdf-ids. However, it is not limited to a particular type of acoustic model.

The program est-lda does the LDA estimation (it reads in the statistics from acc-lda). The features you get from the transform will have unit variance, but not necessarily zero mean. The program est-lda outputs the LDA transformation matrix, and using the option –write-full-matrix you can write out the full matrix without dimensionality reduction (its first rows will be equivalent to the LDA projection matrix). This can be useful when using LDA as an initialization for HLDA.

Frame splicing

Frame splicing (e.g. splicing nine consecutive frames together) is typically done to the raw MFCC features prior to LDA. The program splice-feats does this. A typical line from a script that uses this is the following: 

feats="ark:splice-feats scp:data/train.scp ark:- |
        transform-feats $dir/0.mat ark:- ark:-|"

and the "feats" variable would later be used as an rspecifier (c.f. Specifying Table formats: wspecifiers and rspecifiers) by some program that needs to read features. In this example we don't specify the number of frames to splice together because we are using the defaults (–left-context=4, –right-context=4, or 9 frames in total).

Delta feature computation

Computation of delta features is done by the program add-deltas, which uses the function ComputeDeltas. The delta feature computation has the same default setup as HTK's, i.e. to compute the first delta feature we multiply by the features by a sliding window of values [ -2, -1, 0, 1, 2 ], and then normalize by dividing by (2^2 + 1^2 + 0^2 + 1^2 + 2^2 = 10). The second delta feature is computed by applying the same approach to the first delta feature. The number of frames of context on each side is controlled by –delta-window (default: 2) and the number of delta features to add is controlled by –delta-order (default: 2). A typical script line that uses this is: 

feats="ark:add-deltas --print-args=false scp:data/train.scp ark:- |"

Heteroscedastic Linear Discriminant Analysis (HLDA)

HLDA is a dimension-reducing linear feature projection, estimated using Maximum Likelihood, where "rejected" dimensions are modeled using a global mean and variance, and "accepted" dimensions are modeled with a particular model whose means and variances are estimated via Maximum Likelihood. The form of HLDA that is currently integrated with the tools is as implemented in HldaAccsDiagGmm. It estimates HLDA for GMMs, using a relatively compact form of the statistics. The classes correspond to the Gaussians in the model. Since it does not use a standard estimation method, we will explain the idea here. Firstly, because of memory limitations we do not want to store the largest form of HLDA statistics which is mean and full-covariance statistics for each class. We observe that if during the HLDA update phase we leave the variances fixed, then the problem of HLDA estimation reduces to MLLT (or global STC) estimation. See "Semi-tied Covariance Matrices for Hidden Markov Models", by Mark Gales, IEEE Transactions on Speech and Audio Processing, vol. 7, 1999, pages 272-281, e.g. Equations (22) and (23). The statistics that are 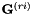$ \mathbf{G}^{(ri)} $ there, are also used here, but in the HLDA case they need to be defined slightly differently for the accepted and rejected dimensions. Suppose the original feature dimension is D and the reduced feature dimension is K. Let us forget the iteration superscript r, and use subscript j for state and m for Gaussian mixture. For accepted dimensions ( $0 \leq i < K$), the statistics are:

\[ \mathbf{G}^{(i)} = \sum_{t,j,m} \gamma_{jm}(t) \frac{1}{ \sigma^2_{jm}(i) } (\mu_{jm} - \mathbf{x}(t)) (\mu_{jm} - \mathbf{x}(t))^T \]

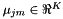where $\mu_{jm} \in \Re^{K}$ is the Gaussian mean in the original D-dimensional space, and 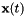$\mathbf{x}(t)$ is the feature in the original K-dimensional space, but 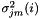$\sigma^2_{jm}(i)$ is the i'th dimension of the variance within the the K-dimensional model.

For rejected dimensions ( 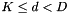$ K \leq d < D$), we use a unit variance Gaussian, and the statistics are as follows:

\[ \mathbf{G}^{(i)} = \sum_{t,j,m} \gamma_{jm}(t) (\mu - \mathbf{x}(t)) (\mu - \mathbf{x}(t))^T , \]

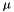where $\mu$ is the global feature mean in the K-dimensional space. Once we have these statistics, HLDA estimation is the same as MLLT/STC estimation in dimension D. Note here that all the $\mathbf{G}$ statistics for rejected dimensions are the same, so in the code we only store statistics for K+1 rather than D dimensions.

Also, it is convenient for the program that accumulates the statistics to only have access to the K-dimensional model, so during HLDA accumulation we accumulate statistics sufficient to estimate the K-dimensional means 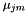$\mu_{jm}$, and insead of G we accumulate the following statistics: for accepted dimensions ( $0 \leq i < K$),

\[ \mathbf{S}^{(i)} = \sum_{t,j,m} \gamma_{jm}(t) \frac{1}{ \sigma^2_{jm}(i) } \mathbf{x}(t) \mathbf{x}(t)^T \]

and for rejected dimensions 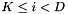$K \leq i < D$

\[ \mathbf{S}^{(i)} = \sum_{t,j,m} \gamma_{jm}(t) \mathbf{x}(t) \mathbf{x}(t)^T , \]

and of course we only need to store one of these (e.g. for i = K) because they are all the same. Then in the update time we can compute the G statistics for 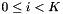$0 \leq i < K$ as:

\[ \mathbf{G}^{(i)} = \mathbf{S}^{(i)} - \sum_{j,m} \gamma_{jm} \mu_{jm} \mu_{jm}^T , \]

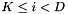and for $K \leq i < D$,

\[ \mathbf{G}^{(i)} = \mathbf{S}^{(i)} - \beta \mu \mu^T, \]

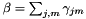where $ \beta = \sum_{j,m} \gamma_{jm} $ is the total count and 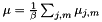$\mu = \frac{1}{\beta} \sum_{j,m} \mu_{j,m}$ is the global feature mean. After computing the transform from the G statistics using the same computation as MLLT, we output the transform, and we also use the first K rows of the transform to project the means into dimension K and write out the transformed model.

The computation described here is fairly slow; it is 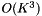$ O(K^3) $ on each frame, and K is fairly large (e.g. 117). This is the price we pay for compact statistics; if we stored full mean and variance statistics, the per-frame computation would be 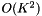$O(K^2)$. To speed it up, we have an optional parameter ("speedup" in the code) which selects a random subset of frames to actually compute the HLDA statistics on. For instance, if speedup=0.1 we would only accumulate HLDA statistics on 1/10 of the frames. If this option is activated, we need to store two separate versions of the sufficient statistics for the means. 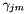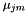One version of the mean statistics, accumulated on the subset, is only used in the HLDA computation, and corresponds to the quantities $\gamma_{jm}$ and $\mu_{jm}$ in the formulas above. The other version of the mean statistics is accumulated on all the training data and is used to write out the transformed model.

The overall HLDA estimation process is as follows (see rm_recipe_2/scripts/train_tri2j.sh):

  • First initialize it with LDA (we store both the reduced dimension matrix and the full matrix).
  • Start model-building and training process. On certain (non-consecutive) iterations where we have decided to do the HLDA update, do the following:
    • Accumulate HLDA statistics (S, plus statistics for the full-dimensional means). The program that accumulates these (gmm-acc-hlda) needs the model, the un-transformed features, and the current transform (which it needs to transform the features in order to compute Gaussian posteriors)
    • Update the HLDA transform. The program that does this (gmm-est-hlda) needs the model; the statistics; and the previous full (square) transformation matrix which it needs to start the optimization and to correctly report auxiliary function changes. It outputs the new transform (both full and reduced dimension), and the model with newly estimated and transformed means.

Global Semi-tied Covariance (STC) / Maximum Likelihood Linear Transform (MLLT) estimation

Global STC/MLLT is a square feature-transformation matrix. For more details, see "Semi-tied Covariance Matrices for Hidden Markov Models", by Mark Gales, IEEE Transactions on Speech and Audio Processing, vol. 7, 1999, pages 272-281. Viewing it as a feature-space transform, the objective function is the average per-frame log-likelihood of the transformed features given the model, plus the log determinant of the transform. The means of the model are also rotated by transform in the update phase. The sufficient statistics are the following, for 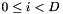$ 0 \leq i < D $ where D is the feature dimension:

\[ \mathbf{G}^{(i)} = \sum_{t,j,m} \gamma_{jm}(t) \frac{1}{ \sigma^2_{jm}(i) } (\mu_{jm} - \mathbf{x}(t)) (\mu_{jm} - \mathbf{x}(t))^T \]

See the reference, Equations (22) and (23) for the update equations. These are basically a simplified form of the diagonal row-by-row Constrained MLLR/fMLLR update equations, where the first-order term of the quadratic equation disappears. Note that our implementation differs from that reference by using a column of the inverse of the matrix rather than the cofactor, since multiplying by the determinant does not make a difference to the result and could potentially cause problems with floating-point underflow or overflow.

We describe the overall process as if we are doing MLLT on top of LDA features, but it is also applicable on top of traditional delta features. See the script rm_recipe_2/steps/train_tri2f for an example. The process is as follows:

  • Estimate the LDA transformation matrix (we only need the first rows of this, not the full matrix). Call this matrix $\mathbf{M}$.
  • Start a normal model building process, always using features transformed with $\mathbf{M}$. At certain selected iterations (where we will update the MLLT matrix), we do the following:
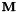    • Accumulate MLLT statistics in the current fully-transformed space (i.e., on top of features transformed with $\mathbf{M}$). For efficiency we do this using a subset of the training data.
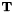    • Do the MLLT update; let this produce a square matrix $\mathbf{T}$.
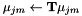    • Transform the model means by setting $ \mu_{jm} \leftarrow \mathbf{T} \mu_{jm} $.
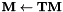
    • Update the current transform by setting $ \mathbf{M} \leftarrow \mathbf{T} \mathbf{M} $

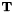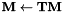The programs involved in MLLT estimation are gmm-acc-mllt and est-mllt. We also need the programs gmm-transform-means (to transform the Gaussian means using $\mathbf{T}$), and compose-transforms (to do the multiplication $\mathbf{M} \leftarrow \mathbf{T} \mathbf{M} $).

Global CMLLR/fMLLR transforms

Constrained Maximum Likelihood Linear Regression (CMLLR), also known as feature-space MLLR (fMLLR), is an affine feature transform of the form 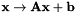$ \mathbf{x} \rightarrow \mathbf{A} \mathbf{x} + \mathbf{b} $, which we write in the form 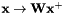$ \mathbf{x} \rightarrow \mathbf{W} \mathbf{x}^+ $, where $\mathbf{x}^+ = \left[\begin{array}{c} \mathbf{x} \\ 1 \end{array} \right]$ is the feature with a 1 appended. Note that this differs from some of the literature where the 1 comes first.

For a review paper that explains CMLLR and the estimation techniques we use, see "Maximum likelihood linear transformations for HMM-based speech recognition" by Mark Gales, Computer Speech and Language Vol. 12, pages 75-98.

The sufficient statistics we store are:

\[ \mathbf{K} = \sum_{t,j,m} \gamma_{j,m}(t) \Sigma_{jm}^{-1} \mu_{jm} \mathbf{x}(t)^+ \]

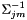where $\Sigma_{jm}^{-1}$ is the inverse covariance matrix, and for 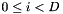$0 \leq i < D $ where D is the feature dimension,

\[ \mathbf{G}^{(i)} = \sum_{t,j,m} \gamma_{j,m}(t) \frac{1}{\sigma^2_{j,m}(i)} \mathbf{x}(t)^+ \left.\mathbf{x}(t)^+\right.^T \]

Our estimation scheme is the standard one, see Appendix B of the reference (in particular section B.1, "Direct method over rows"). We differ by using a column of the inverse in place of the cofactor row, i.e. ignoring the factor of the determinant, as it does not affect the result and causes danger of numerical underflow or overflow.

Estimation of global Constrained MLLR (CMLLR) transforms is done by the class FmllrDiagGmmAccs, and by the program gmm-est-fmllr (also see gmm-est-fmllr-gpost). The syntax of gmm-est-fmllr is: 

gmm-est-fmllr [options] <model-in> <feature-rspecifier> \
   <post-rspecifier> <transform-wspecifier>

The "<post-rspecifier>" item corresponds to posteriors at the transition-id level (see State-level posteriors). The program writes out a table of CMLLR transforms indexed by utterance by default, or if the –spk2utt option is given, indexed by speaker.

Below is a simplified extract of a script (rm_recipe_2/steps/decode_tri_fmllr.sh) that estimates and uses CMLLR transforms based on alignments from a previous, unadapted decoding. The previous decoding is assumed to be with the same model (otherwise we would have to convert the alignments with the program "convert-ali"). 

...
silphones=48 # colon-separated list with one phone-id in it.
mincount=500 # min-count to estimate an fMLLR transform
sifeats="ark:add-deltas --print-args=false scp:data/test.scp ark:- |"

# The next comand computes the fMLLR transforms.
ali-to-post ark:$srcdir/test.ali ark:- | \
  weight-silence-post 0.0 $silphones $model ark:- ark:- | \
  gmm-est-fmllr --fmllr-min-count=$mincount \
    --spk2utt=ark:data/test.spk2utt $model "$sifeats" \
   ark,o:- ark:$dir/test.fmllr 2>$dir/fmllr.log

feats="ark:add-deltas --print-args=false scp:data/test.scp ark:- |
  transform-feats --utt2spk=ark:data/test.utt2spk ark:$dir/test.fmllr
       ark:- ark:- |"

# The next command decodes the data.
gmm-decode-faster --beam=30.0 --acoustic-scale=0.08333 \
  --word-symbol-table=data/words.txt $model $graphdir/HCLG.fst \
 "$feats" ark,t:$dir/test.tra ark,t:$dir/test.ali 2>$dir/decode.log

Linear VTLN (LVTLN)

In recent years, there have been a number of papers that describe implementations of Vocal Tract Length Normalization (VTLN) that work out a linear feature transform corresponding to each VTLN warp factor. See, for example, ``Using VTLN for broadcast news transcription'', by D. Y. Kim, S. Umesh, M. J. F. Gales, T. Hain and P. C. Woodland, ICSLP 2004.

We implement a method in this general category using the class LinearVtln, and programs such as gmm-init-lvtln, gmm-train-lvtln-special, and gmm-est-lvtln-trans. The LinearVtln object essentially stores a set of linear feature transforms, one for each warp factor. Let these linear feature transform matrices be

\[\mathbf{A}^{(i)}, 0\leq i < N, \]

where for instance we might have 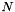$N$=31, corresponding to 31 different warp factors. We will describe below how we obtain these matrices below. The way the speaker-specific transform is estimated is as follows. First, we require some kind of model and a corresponding alignment. In the example scripts we do this either with a small monophone model, or with a full triphone model. From this model and alignment, and using the original, unwarped features, we compute the conventional statistics for estimating CMLLR. When computing the LVTLN transform, what we do is take each matrix 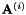$\mathbf{A}^{(i)}$, and compute the offset vector 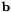$\mathbf{b}$ that maximizes the CMLLR auxiliary function for the transform $\mathbf{W} = \left[ \mathbf{A}^{(i)} \, ; \, \mathbf{b} \right]$. 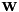This value of $\mathbf{W}$ that gave the best auxiliary function value (i.e. maximizing over i) becomes the transform for that speaker. Since we are estimating a mean offset here, we are essentially combining a kind of model-based cepstral mean normalization (or alternatively an offset-only form of CMLLR) with VTLN warping implemented as a linear transform. This avoids us having to implement mean normalization as a separate step.

We next describe how we estimate the matrices 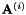$\mathbf{A}^{(i)}$. We don't do this in the same way as described in the referenced paper; our method is simpler (and easier to justify). Here we describe our computation for a particular warp factor; in the current scripts we have 31 distinct warp factors ranging from 0.85, 0.86, ..., 1.15. We take a subset of feature data (e.g. several tens of utterances), and for this subset we compute both the original and transformed features, where the transformed features are computed using a conventional VLTN computation (see Feature-level Vocal Tract Length Normalization (VTLN).). 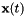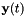Call the original and transformed features $\mathbf{x}(t)$ and $\mathbf{y}(t)$ respectively, where 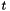$t$ will range over the frames of the selected utterances. 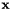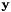We compute the affine transform that maps $\mathbf{x}$ to $\mathbf{y}$ in a least-squares sense, i.e. 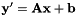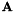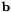if $\mathbf{y}' = \mathbf{A} \mathbf{x} + \mathbf{b}$, we compute $\mathbf{A}$ and $\mathbf{b}$ that minimizes the sum-of-squares difference 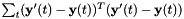$\sum_t (\mathbf{y}'(t) - \mathbf{y}(t) )^T (\mathbf{y}'(t) - \mathbf{y}(t) )$. 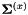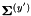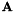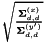Then we normalize the diagonal variance as follows: we compute the variance of the original features as $\mathbf{\Sigma}^{(x)}$ and of the linearly transformed features as $\mathbf{\Sigma}^{(y')}$, and for each dimension index d we multiply the d'th row of $\mathbf{A}$ by $\sqrt{ \frac{\mathbf{\Sigma}^{(x)}_{d,d}}{\mathbf{\Sigma}^{(y')}_{d,d}}}$. The resulting matrix will become 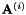$\mathbf{A}^{(i)}$ for some value of i.

The command-line tools support the option to ignore the log determinant term when evaluating which of the transform matrices to use (e.g., you can set –logdet-scale=0.0). Under certain circumstances this appears to improve results; ignoring the log determinant it always makes the distribution of warp factors more bimodal because the log determinant is never positive and is zero for a warp factor of 1.0, so the log determinant essentially acts as a penalty on warp factors that are far away from 1. However, for certain types of features (in particular, features derived from LDA), ignoring the log determinant makes results a lot worse and leads to very odd distributions of warp factors, so our example scripts always use the log-determinant. This is anyway the "right" thing to do.

The internal C++ code supports accumluating statistics for Maximum Likelihood re-estimation of the transform matrices 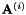$\mathbf{A}^{(i)}$. Our expectation was that this would improve results. However, it led to a degradation in performance so we do not include example scripts for doing this.

Exponential Transform (ET)

The Exponential Transform (ET) is another approach to computing a VTLN-like transform, but unlike Linear VTLN we completely sever the connection to frequency warping, and learn it in a data-driven way. For normal training data, we find that it does learn something very similar to conventional VTLN.

ET is a transform of the form:

\[ \mathbf{W}_s = \mathbf{D}_s \exp ( t_s \mathbf{A} ) \mathbf{B} , \]

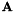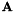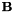where exp is the matrix exponential function, defined via a Taylor series in $\mathbf{A}$ that is the same as the Taylor series for the scalar exponential function. Quantities with a subscript "s" are speaker-specific; other quantities (i.e. $\mathbf{A}$ and $\mathbf{B}$) are global and shared across all speakers.

The most important factor in this equation is the middle one, with the exponential function in it. The factor 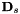$\mathbf{D}_s$ gives us the ability to combine model-based mean and optionally variance normalization (i.e. offset-only or diagonal-only CMLLR) with this technique, and the factor 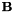$\mathbf{B}$ allows the transform to include MLLT (a.k.a. global STC), and is also a byproduct of the process of renormalizing the 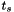$t_s$ quantities on each iteration of re-estimation. The dimensions of these quantities are as follows, where D is the feature dimension:

\[ \mathbf{D}_s \in \Re^{D \times (D+1)}, \ t_s \in \Re, \ \mathbf{A} \in \Re^{(D+1)\times(D+1)}, \ \mathbf{B} \in \Re^{(D+1)\times (D+1)} . \]

Note that if 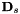$\mathbf{D}_s$ were a completely unconstrained CMLLR matrix, there would be no point to this technique as the other quantities in the equation would add no degrees of freedom. The tools support three kinds of constraints on 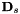$\mathbf{D}_s$: it may be of the form $[ {\mathbf I} \, \;\, {\mathbf 0} ]$ (no adaptation), or $[ {\mathbf I} \, \;\, {\mathbf m} ]$ (offset only), or $[ {\mathrm{diag}}( {\mathbf d} ) \, \;\, {\mathbf m} ]$ (diagonal CMLLR); this is controlled by the –normalize-type options to the command-line tools. 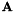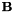The last rows of $\mathbf{A}$ and $\mathbf{B}$ are fixed at particular values (these rows are involved in propagating the last vector element with value 1.0, which is appended to the feature in order to express an affine transform as a matrix). The last row of 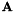$\mathbf{A}$ is fixed at zero and the last row of 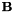$\mathbf{B}$ is fixed at $[ 0\ 0\ 0 \ \ldots\ 0 \ 1]$.

The speaker-specific quantity 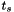$t_s$ may be interpreted very loosely as the log of the speaker-specific warp factor. The basic intuition behind the use of the exponential function is that if we were to warp by a factor f and then a factor g, this should be the same as warping by the combined factor fg. Let l = log(f) and m = log(g). Then we achieve this property via the identity

\[ \exp( l \mathbf{A} ) \exp( m \mathbf{A}) = \exp( (l+m) \mathbf{A} ) . \]

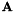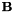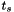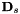The ET computation for a particular speaker is as follows; this assumes we are given $\mathbf{A}$ and $\mathbf{B}$. We accumulate conventional CMLLR sufficient statistics for the speaker. In the update phase we iteratively optimize $t_s$ and $\mathbf{D}_s$ to maximize the auxiliary function. 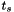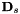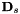The update for $t_s$ is an iterative procedure based on Newton's method; the update for $\mathbf{D}_s$ is based on the conventional CMLLR update, specialized for the diagonal or offset-only case, depending on the exact constraints we are putting $\mathbf{D}_s$.

The overall training-time computation is as follows:

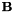  • First, initialize $\mathbf{B}$ to the identity and 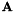$\mathbf{A}$ to a random matrix with zero final row.

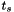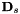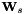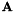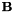Then, starting with some known model, start an iterative E-M process. On each iteration, we first estimate the speaker-specific parameters $t_s$ and $\mathbf{D}_s$, and compute the transforms $\mathbf{W}_s$ that result from them. Then we choose to update either $\mathbf{A}$, or $\mathbf{B}$, or the model.

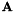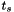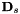  • If updating $\mathbf{A}$, we do this given fixed values of $t_s$ and $\mathbf{D}_s$. The update is not guaranteed to converge, but converges rapidly in practice; it's based on a quadratic "weak-sense auxiliary function" where the quadratic term is obtained using a first-order truncation of the Taylor series expansion of the matrix exponential function. 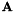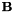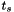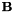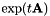After updating $\mathbf{A}$, we modify $\mathbf{B}$ in order to renormalize the $t_s$ to zero; this involves premultiplying $\mathbf{B}$ by $\exp(t \mathbf{A})$, where t is the average value of $t_s$.
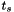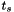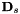  • If updating $\mathbf{B}$, this is also done using fixed values of $t_s$ and $\mathbf{D}_s$, and the update is similar to MLLT (a.k.a. global STC). For purposes of the accumulation and update, we imagine we are estimating an MLLT matrix just to the left of 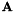$\mathbf{A}$, i.e. some matrix 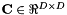$\mathbf{C} \in \Re^{D\times D}$; let us define $\mathbf{C}^+ = \left[ \begin{array}{cc} \mathbf{C} & 0 \\ 0 & 1 \end{array} \right]$. 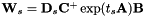The transform will be $\mathbf{W}_s = \mathbf{D}_s \mathbf{C}^+ \exp ( t_s \mathbf{A} ) \mathbf{B}$. Conceptually, while estimating 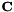$\mathbf{C}$ we view 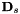$\mathbf{D}_s$ as a model-space transform creating speaker-specific models, which this is only possible due to the diagonal structure of 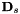$\mathbf{D}_s$; and we view 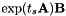$\exp ( t_s \mathbf{A} ) \mathbf{B}$ as a feature-space transform (i.e. as part of the features). After estimating 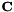$\mathbf{C}$, we will use the identity

    \[ \mathbf{C}^+ \exp ( t_s \mathbf{A} ) = \exp ( t_s \mathbf{C}^+ \mathbf{A} \left.\mathbf{C}^+\right.^{-1} ) \mathbf{C}^+ \]

    so the update becomes:

    \[ \mathbf{A} \leftarrow \mathbf{C}^+ \mathbf{A} \left.\mathbf{C}^+\right.^{-1} , \ \ \mathbf{B} \leftarrow \mathbf{C}^+ \mathbf{B} . \]

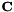    At this point we need to transform the model means with the matrix $\mathbf{C}$. The reader might question how this interacts with the fact that for estimating 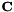$\mathbf{C}$, we viewed the quantity 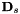$\mathbf{D}_s$ as a model-space transform. If 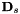$\mathbf{D}_s$ only contains a mean offset, we can still prove that the auxiliary function would increase, except we would have to change the offsets appropriately (this is not necessary to do explicitly, as we will re-estimate them on the next iteration anyway). However, if 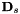$\mathbf{D}_s$ has non-unit diagonal (i.e. is diagonal not offset CMLLR), this re-estimation process is not guaranteed to improve the likelihood; the tools will print a warning in this case. In order to avoid encountering this case, our scripts train in a mode where 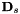$\mathbf{D}_s$ is an offset-only transform; but in test time we allow 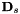$\mathbf{D}_s$ to be a diagonal CMLLR transform, which seems to give slightly better results than the offset-only case.
  • Updating the model is straightforward; it just involves training on the adapted features.

Important programs related to the use of exponential transforms are as follows:

  • gmm-init-et initializes the exponential transform object (that contains A and B) and writes it to disk; the initialization of A is random.
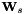  • gmm-est-et estimates the exponential transforms for a set of speakers; it reads the exponential transform object, the model, the features and Gaussian-level posteriors, and it writes out the transforms $\mathbf{W}_s$ and optionally the "warp factors" $t_s$.
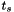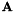  • gmm-et-acc-a accumulates statistics for updating $\mathbf{A}$, and and gmm-et-est-a does the corresponding update.
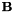  • gmm-et-acc-b accumulates statistics for updating $\mathbf{B}$, and and gmm-et-est-b does the corresponding update.

Cepstral mean and variance normalization

Cepstral mean and variance normalization consists of normalizing the mean and variance of the raw cepstra, usually to give zero-mean, unit-variance cepstra, either on a per-utterance or per-speaker basis. We provide code to support this, and some example scripts, but we do not particularly recommend its use. In general we prefer model-based approaches to mean and variance normalization; e.g., our code for Linear VTLN (LVTLN) also learns a mean offset and the code for Exponential Transform (ET) does a diagonal CMLLR transform that has the same power as cepstral mean and variance normalization (except usually applied to the fully expanded features). For very fast operation, it is possible to apply these approaches using a very tiny model with a phone-based language model, and some of our example scripts demonstrate this. There is also the capability in the feature extraction code to subtract the mean on a per-utterance basis (the –subtract-mean option to compute-mfcc-feats and compute-plp-feats).

In order to support per-utterance and per-speaker mean and variance normalization we provide the programs compute-cmvn-stats and apply-cmvn. The program compute-cmvn-stats will, by default, compute the sufficient statistics for mean and variance normalization, as a matrix (the format is not very important; see the code for details), and will write out a table of these statistics indexed by utterance-id. If it is given the –spk2utt option, it will write out the statistics on a per-speaker basis instead (warning: before using this option, read Avoiding memory bloat when reading archives in random-access mode, as this option causes the input features to be read in random-access mode). The program "apply-cmvn" reads in features and cepstral mean and variance statistics; the statistics are expected to be indexed per utterance by default, or per speaker if the –utt2spk option is applied. It writes out the features after mean and variance normalization. These programs, despite the names, do not care whether the features in question consist of cepstra or anything else; it simply regards them as matrices. Of course, the features supplied to compute-cmvn-stats and apply-cmvn must have the same dimension.

We note that it would probably be more consistent with the overall design of the feature transformation code, to supply a version of compute-cmvn-stats that would write write out the mean and variance normalizing transforms as generic affine transforms (in the same format as CMLLR transforms), so that they could be applied by the program transform-feats, and composed as needed with other transforms using compose-transforms. If needed we may supply such a program, but because we don't regard mean and variance normalization as an important part of any recipes, we have not done so yet.

Building regression trees for adaptation

Kaldi supports regression-tree MLLR and CMLLR (also known as fMLLR). For an overview of regression trees, see "The generation and use of regression class trees for MLLR adaptation" by M. J. F. Gales, CUED technical report, 1996.