Plda Class Reference

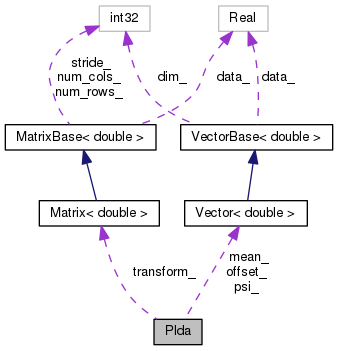
#include <plda.h>

Collaboration diagram for Plda:

Public Member Functions
	Plda ()
	Plda (const Plda &other)
double	TransformIvector (const PldaConfig &config, const VectorBase< double > &ivector, int32 num_enroll_examples, VectorBase< double > *transformed_ivector) const
	Transforms an iVector into a space where the within-class variance is unit and between-class variance is diagonalized. More...
float	TransformIvector (const PldaConfig &config, const VectorBase< float > &ivector, int32 num_enroll_examples, VectorBase< float > *transformed_ivector) const
	float version of the above (not BaseFloat because we'd be implementing it twice for the same type if BaseFloat == double). More...
double	LogLikelihoodRatio (const VectorBase< double > &transformed_enroll_ivector, int32 num_enroll_utts, const VectorBase< double > &transformed_test_ivector) const
	Returns the log-likelihood ratio log (p(test_ivector | same) / p(test_ivector | different)). More...
void	SmoothWithinClassCovariance (double smoothing_factor)
	This function smooths the within-class covariance by adding to it, smoothing_factor (e.g. More...
void	ApplyTransform (const Matrix< double > &in_transform)
	Apply a transform to the PLDA model. More...
int32	Dim () const
void	Write (std::ostream &os, bool binary) const
void	Read (std::istream &is, bool binary)

Protected Member Functions
void	ComputeDerivedVars ()

Protected Attributes
Vector< double >	mean_
Matrix< double >	transform_
Vector< double >	psi_
Vector< double >	offset_

Private Member Functions
Plda &	operator= (const Plda &other)
double	GetNormalizationFactor (const VectorBase< double > &transformed_ivector, int32 num_examples) const
	This returns a normalization factor, which is a quantity we must multiply "transformed_ivector" by so that it has the length that it "should" have. More...

Friends
class	PldaEstimator
class	PldaUnsupervisedAdaptor

Detailed Description

Definition at line 74 of file plda.h.

Constructor & Destructor Documentation

Plda() [1/2]

Plda ( )

inline

Definition at line 76 of file plda.h.

{ }

Plda() [2/2]

Plda ( const Plda &  other )

inlineexplicit

Definition at line 78 of file plda.h.

                                  :
    mean_(other.mean_),
    transform_(other.transform_),
    psi_(other.psi_),
    offset_(other.offset_) {
  };

Member Function Documentation

ApplyTransform()

void ApplyTransform

(

const Matrix< double > &

in_transform

)

Apply a transform to the PLDA model.

This is mostly used for projecting the parameters of the model into a lower dimensional space, i.e. in_transform.NumRows() <= in_transform.NumCols(), typically for speaker diarization with a PCA transform.

Definition at line 220 of file plda.cc.

References SpMatrix< Real >::AddMat2Sp(), MatrixBase< Real >::AddMatMat(), VectorBase< Real >::AddMatVec(), VectorBase< Real >::ApplyFloor(), Plda::ComputeDerivedVars(), kaldi::ComputeNormalizingTransform(), VectorBase< Real >::CopyFromVec(), Plda::Dim(), SpMatrix< Real >::Eig(), SpMatrix< Real >::Invert(), KALDI_ASSERT, KALDI_WARN, kaldi::kNoTrans, kaldi::kTrans, Plda::mean_, VectorBase< Real >::Min(), rnnlm::n, MatrixBase< Real >::NumCols(), MatrixBase< Real >::NumRows(), Plda::psi_, Vector< Real >::Resize(), Matrix< Real >::Resize(), kaldi::SortSvd(), and Plda::transform_.

Referenced by main().

                                                            {
  KALDI_ASSERT(in_transform.NumRows() <= Dim()
    && in_transform.NumCols() == Dim());

  // Apply in_transform to mean_.
  Vector<double> mean_new(in_transform.NumRows());
  mean_new.AddMatVec(1.0, in_transform, kNoTrans, mean_, 0.0);
  mean_.Resize(in_transform.NumRows());
  mean_.CopyFromVec(mean_new);

  SpMatrix<double> between_var(in_transform.NumCols()),
                   within_var(in_transform.NumCols()),
                   psi_mat(in_transform.NumCols()),
                   between_var_new(Dim()),
                   within_var_new(Dim());
  Matrix<double> transform_invert(transform_);

  // Next, compute the between_var and within_var that existed
  // prior to diagonalization.
  psi_mat.AddDiagVec(1.0, psi_);
  transform_invert.Invert();
  within_var.AddMat2(1.0, transform_invert, kNoTrans, 0.0);
  between_var.AddMat2Sp(1.0, transform_invert, kNoTrans, psi_mat, 0.0);

  // Next, transform the variances using the input transformation.
  between_var_new.AddMat2Sp(1.0, in_transform, kNoTrans, between_var, 0.0);
  within_var_new.AddMat2Sp(1.0, in_transform, kNoTrans, within_var, 0.0);

  // Finally, we need to recompute psi_ and transform_. The remainder of
  // the code in this function  is a lightly modified copy of
  // PldaEstimator::GetOutput().
  Matrix<double> transform1(Dim(), Dim());
  ComputeNormalizingTransform(within_var_new, &transform1);
  // Now transform is a matrix that if we project with it,
  // within_var becomes unit.
  // between_var_proj is between_var after projecting with transform1.
  SpMatrix<double> between_var_proj(Dim());
  between_var_proj.AddMat2Sp(1.0, transform1, kNoTrans, between_var_new, 0.0);

  Matrix<double> U(Dim(), Dim());
  Vector<double> s(Dim());
  // Do symmetric eigenvalue decomposition between_var_proj = U diag(s) U^T,
  // where U is orthogonal.
  between_var_proj.Eig(&s, &U);

  KALDI_ASSERT(s.Min() >= 0.0);
  int32 n;
  s.ApplyFloor(0.0, &n);
  if (n > 0) {
    KALDI_WARN << "Floored " << n << " eigenvalues of between-class "
               << "variance to zero.";
  }
  // Sort from greatest to smallest eigenvalue.
  SortSvd(&s, &U);

  // The transform U^T will make between_var_proj diagonal with value s
  // (i.e. U^T U diag(s) U U^T = diag(s)).  The final transform that
  // makes within_var unit and between_var diagonal is U^T transform1,
  // i.e. first transform1 and then U^T.
  transform_.Resize(Dim(), Dim());
  transform_.AddMatMat(1.0, U, kTrans, transform1, kNoTrans, 0.0);
  psi_.Resize(Dim());
  psi_.CopyFromVec(s);
  ComputeDerivedVars();
}

ComputeDerivedVars()

void ComputeDerivedVars ( )

protected

Definition at line 57 of file plda.cc.

References VectorBase< Real >::AddMatVec(), Plda::Dim(), KALDI_ASSERT, kaldi::kNoTrans, Plda::mean_, Plda::offset_, Vector< Real >::Resize(), and Plda::transform_.

Referenced by Plda::ApplyTransform(), PldaEstimator::GetOutput(), Plda::Read(), and Plda::SmoothWithinClassCovariance().

                              {
  KALDI_ASSERT(Dim() > 0);
  offset_.Resize(Dim());
  offset_.AddMatVec(-1.0, transform_, kNoTrans, mean_, 0.0);
}

Dim()

int32 Dim ( ) const

inline

Definition at line 140 of file plda.h.

Referenced by Plda::ApplyTransform(), Plda::ComputeDerivedVars(), Plda::GetNormalizationFactor(), Plda::LogLikelihoodRatio(), main(), Plda::SmoothWithinClassCovariance(), Plda::TransformIvector(), kaldi::TransformIvectors(), and PldaUnsupervisedAdaptor::UpdatePlda().

{ return mean_.Dim(); }

GetNormalizationFactor()

double GetNormalizationFactor ( const VectorBase< double > &  transformed_ivector, int32  num_examples  ) const

private

This returns a normalization factor, which is a quantity we must multiply "transformed_ivector" by so that it has the length that it "should" have.

This comment explains the thinking behind the function LogLikelihoodRatio.

We assume "transformed_ivector" is an iVector in the transformed space (i.e., mean-subtracted, and multiplied by transform_). The covariance it "should" have in this space is + I/num_examples.

The reference is "Probabilistic Linear Discriminant Analysis" by Sergey Ioffe, ECCV 2006.

I'm looking at the un-numbered equation between eqs. (4) and (5), that says P(u^p | u^g_{1...n}) = N (u^p | {n }{n + I} {u}^g, I + {}{n + I})

Here, the superscript ^p refers to the "probe" example (e.g. the example to be classified), and u^g_1 is the first "gallery" example, i.e. the first training example of that class. is the between-class covariance matrix, assumed to be diagonalized, and I can be interpreted as the within-class covariance matrix which we have made unit.

We want the likelihood ratio P(u^p | u^g_{1..n}) / P(u^p), where the numerator is the probability of u^p given that it's in that class, and the denominator is the probability of u^p with no class assumption at all (e.g. in its own class).

The expression above even works for n = 0 (e.g. the denominator of the likelihood ratio), where it gives us P(u^p) = N(u^p | 0, I + ) i.e. it's distributed with zero mean and covarance (within + between). The likelihood ratio we want is: N(u^p | {n }{n + I} {u}^g, I + {}{n + I}) / N(u^p | 0, I + ) where {u}^g is the mean of the "gallery examples"; and we can expand the log likelihood ratio as

• 0.5 [ (u^p - m) (I + /(n + I))^{-1} (u^p - m) + logdet(I + /(n + I)) ] + 0.5 [u^p (I + ) u^p + logdet(I + ) ] where m = (n )/(n + I) {u}^g.

Definition at line 99 of file plda.cc.

References VectorBase< Real >::Add(), VectorBase< Real >::ApplyPow(), Plda::Dim(), VectorBase< Real >::InvertElements(), KALDI_ASSERT, Plda::psi_, and kaldi::VecVec().

Referenced by Plda::TransformIvector().

                              {
  KALDI_ASSERT(num_examples > 0);
  // Work out the normalization factor.  The covariance for an average over
  // "num_examples" training iVectors equals \Psi + I/num_examples.
  Vector<double> transformed_ivector_sq(transformed_ivector);
  transformed_ivector_sq.ApplyPow(2.0);
  // inv_covar will equal 1.0 / (\Psi + I/num_examples).
  Vector<double> inv_covar(psi_);
  inv_covar.Add(1.0 / num_examples);
  inv_covar.InvertElements();
  // "transformed_ivector" should have covariance (\Psi + I/num_examples), i.e.
  // within-class/num_examples plus between-class covariance.  So
  // transformed_ivector_sq . (I/num_examples + \Psi)^{-1} should be equal to
  //  the dimension.
  double dot_prod = VecVec(inv_covar, transformed_ivector_sq);
  return sqrt(Dim() / dot_prod);
}

LogLikelihoodRatio()

double LogLikelihoodRatio	(	const VectorBase< double > &	transformed_enroll_ivector,
		int32	num_enroll_utts,
		const VectorBase< double > &	transformed_test_ivector
	)		const

Returns the log-likelihood ratio log (p(test_ivector | same) / p(test_ivector | different)).

transformed_enroll_ivector is an average over utterances for that speaker. Both transformed_enroll_vector and transformed_test_ivector are assumed to have been transformed by the function TransformIvector(). Note: any length normalization will have been done while computing the transformed iVectors.

Definition at line 153 of file plda.cc.

References VectorBase< Real >::Add(), VectorBase< Real >::AddVec(), VectorBase< Real >::ApplyPow(), Plda::Dim(), rnnlm::i, VectorBase< Real >::InvertElements(), kaldi::kUndefined, M_LOG_2PI, Plda::psi_, VectorBase< Real >::SumLog(), and kaldi::VecVec().

Referenced by main().

                                                              {
  int32 dim = Dim();
  double loglike_given_class, loglike_without_class;
  { // work out loglike_given_class.
    // "mean" will be the mean of the distribution if it comes from the
    // training example.  The mean is \frac{n \Psi}{n \Psi + I} \bar{u}^g
    // "variance" will be the variance of that distribution, equal to
    // I + \frac{\Psi}{n\Psi + I}.
    Vector<double> mean(dim, kUndefined);
    Vector<double> variance(dim, kUndefined);
    for (int32 i = 0; i < dim; i++) {
      mean(i) = n * psi_(i) / (n * psi_(i) + 1.0)
        * transformed_train_ivector(i);
      variance(i) = 1.0 + psi_(i) / (n * psi_(i) + 1.0);
    }
    double logdet = variance.SumLog();
    Vector<double> sqdiff(transformed_test_ivector);
    sqdiff.AddVec(-1.0, mean);
    sqdiff.ApplyPow(2.0);
    variance.InvertElements();
    loglike_given_class = -0.5 * (logdet + M_LOG_2PI * dim +
                                  VecVec(sqdiff, variance));
  }
  { // work out loglike_without_class.  Here the mean is zero and the variance
    // is I + \Psi.
    Vector<double> sqdiff(transformed_test_ivector); // there is no offset.
    sqdiff.ApplyPow(2.0);
    Vector<double> variance(psi_);
    variance.Add(1.0); // I + \Psi.
    double logdet = variance.SumLog();
    variance.InvertElements();
    loglike_without_class = -0.5 * (logdet + M_LOG_2PI * dim +
                                    VecVec(sqdiff, variance));
  }
  double loglike_ratio = loglike_given_class - loglike_without_class;
  return loglike_ratio;
}

operator=()

Plda& operator= ( const Plda &  other )

private

Read()

void Read	(	std::istream &	is,
		bool	binary
	)

Definition at line 34 of file plda.cc.

References Plda::ComputeDerivedVars(), kaldi::ExpectToken(), Plda::mean_, Plda::psi_, Vector< Real >::Read(), Matrix< Real >::Read(), and Plda::transform_.

                                           {
  ExpectToken(is, binary, "<Plda>");
  mean_.Read(is, binary);
  transform_.Read(is, binary);
  psi_.Read(is, binary);
  ExpectToken(is, binary, "</Plda>");
  ComputeDerivedVars();
}

SmoothWithinClassCovariance()

void SmoothWithinClassCovariance

(

double

smoothing_factor

)

This function smooths the within-class covariance by adding to it, smoothing_factor (e.g.

0.1) times the between-class covariance (it's implemented by modifying transform_). This is to compensate for situations where there were too few utterances per speaker get a good estimate of the within-class covariance, and where the leading elements of psi_ were as a result very large.

We now revise our estimate of the within-class covariance to this larger value. This means that the transform has to change to as to make this new, larger covariance unit. And our between-class covariance in this space is now less.

Definition at line 195 of file plda.cc.

References VectorBase< Real >::AddVec(), VectorBase< Real >::ApplyPow(), Plda::ComputeDerivedVars(), Plda::Dim(), KALDI_ASSERT, KALDI_LOG, MatrixBase< Real >::MulRowsVec(), Plda::psi_, VectorBase< Real >::Set(), and Plda::transform_.

Referenced by main().

                                                              {
  KALDI_ASSERT(smoothing_factor >= 0.0 && smoothing_factor <= 1.0);
  // smoothing_factor > 1.0 is possible but wouldn't really make sense.

  KALDI_LOG << "Smoothing within-class covariance by " << smoothing_factor
            << ", Psi is initially: " << psi_;
  Vector<double> within_class_covar(Dim());
  within_class_covar.Set(1.0); // It's now the current within-class covariance
                               // (a diagonal matrix) in the space transformed
                               // by transform_.
  within_class_covar.AddVec(smoothing_factor, psi_);

  psi_.DivElements(within_class_covar);
  KALDI_LOG << "New value of Psi is " << psi_;

  within_class_covar.ApplyPow(-0.5);
  transform_.MulRowsVec(within_class_covar);

  ComputeDerivedVars();
}

TransformIvector() [1/2]

double TransformIvector	(	const PldaConfig &	config,
		const VectorBase< double > &	ivector,
		int32	num_enroll_examples,
		VectorBase< double > *	transformed_ivector
	)		const

Transforms an iVector into a space where the within-class variance is unit and between-class variance is diagonalized.

The only anticipated use of this function is to pre-transform iVectors before giving them to the function LogLikelihoodRatio (it's done this way for efficiency because a given iVector may be used multiple times in LogLikelihoodRatio and we don't want to repeat the matrix multiplication

If config.normalize_length == true, it will also normalize the iVector's length by multiplying by a scalar that ensures that ivector^T inv_var ivector = dim. In this case, "num_enroll_examples" comes into play because it affects the expected covariance matrix of the iVector. The normalization factor is returned, even if config.normalize_length == false, in which case the normalization factor is computed but not applied. If config.simple_length_normalization == true, then an alternative normalization factor is computed that causes the iVector length to be equal to the square root of the iVector dimension.

Definition at line 120 of file plda.cc.

References VectorBase< Real >::AddMatVec(), VectorBase< Real >::CopyFromVec(), VectorBase< Real >::Dim(), Plda::Dim(), Plda::GetNormalizationFactor(), KALDI_ASSERT, kaldi::kNoTrans, VectorBase< Real >::Norm(), PldaConfig::normalize_length, Plda::offset_, VectorBase< Real >::Scale(), PldaConfig::simple_length_norm, and Plda::transform_.

Referenced by main(), Plda::TransformIvector(), and kaldi::TransformIvectors().

                                                                             {
  KALDI_ASSERT(ivector.Dim() == Dim() && transformed_ivector->Dim() == Dim());
  double normalization_factor;
  transformed_ivector->CopyFromVec(offset_);
  transformed_ivector->AddMatVec(1.0, transform_, kNoTrans, ivector, 1.0);
  if (config.simple_length_norm)
    normalization_factor = sqrt(transformed_ivector->Dim())
      / transformed_ivector->Norm(2.0);
  else
    normalization_factor = GetNormalizationFactor(*transformed_ivector,
                                                  num_examples);
  if (config.normalize_length)
    transformed_ivector->Scale(normalization_factor);
  return normalization_factor;
}

TransformIvector() [2/2]

float TransformIvector	(	const PldaConfig &	config,
		const VectorBase< float > &	ivector,
		int32	num_enroll_examples,
		VectorBase< float > *	transformed_ivector
	)		const

float version of the above (not BaseFloat because we'd be implementing it twice for the same type if BaseFloat == double).

Definition at line 140 of file plda.cc.

References VectorBase< Real >::CopyFromVec(), VectorBase< Real >::Dim(), and Plda::TransformIvector().

                                                                           {
  Vector<double> tmp(ivector), tmp_out(ivector.Dim());
  float ans = TransformIvector(config, tmp, num_examples, &tmp_out);
  transformed_ivector->CopyFromVec(tmp_out);
  return ans;
}

Write()

void Write	(	std::ostream &	os,
		bool	binary
	)		const

Definition at line 26 of file plda.cc.

References Plda::mean_, Plda::psi_, Plda::transform_, VectorBase< Real >::Write(), MatrixBase< Real >::Write(), and kaldi::WriteToken().

                                                  {
  WriteToken(os, binary, "<Plda>");
  mean_.Write(os, binary);
  transform_.Write(os, binary);
  psi_.Write(os, binary);
  WriteToken(os, binary, "</Plda>");
}

Friends And Related Function Documentation

PldaEstimator

friend class PldaEstimator

friend

Definition at line 145 of file plda.h.

PldaUnsupervisedAdaptor

friend class PldaUnsupervisedAdaptor

friend

Definition at line 146 of file plda.h.

Member Data Documentation

mean_

Vector<double> mean_

protected

Definition at line 148 of file plda.h.

Referenced by Plda::ApplyTransform(), Plda::ComputeDerivedVars(), PldaEstimator::GetOutput(), Plda::Read(), PldaUnsupervisedAdaptor::UpdatePlda(), and Plda::Write().

offset_

Vector<double> offset_

protected

Definition at line 155 of file plda.h.

Referenced by Plda::ComputeDerivedVars(), and Plda::TransformIvector().

psi_

Vector<double> psi_

protected

Definition at line 152 of file plda.h.

Referenced by Plda::ApplyTransform(), Plda::GetNormalizationFactor(), PldaEstimator::GetOutput(), Plda::LogLikelihoodRatio(), Plda::Read(), Plda::SmoothWithinClassCovariance(), PldaUnsupervisedAdaptor::UpdatePlda(), and Plda::Write().

transform_

Matrix<double> transform_

protected

Definition at line 149 of file plda.h.

Referenced by Plda::ApplyTransform(), Plda::ComputeDerivedVars(), PldaEstimator::GetOutput(), Plda::Read(), Plda::SmoothWithinClassCovariance(), Plda::TransformIvector(), PldaUnsupervisedAdaptor::UpdatePlda(), and Plda::Write().

---

The documentation for this class was generated from the following files:

• ivector/plda.h
• ivector/plda.cc