PldaUnsupervisedAdaptor Class Reference

This class takes unlabeled iVectors from the domain of interest and uses their mean and variance to adapt your PLDA matrices to a new domain. More...

#include <plda.h>

Collaboration diagram for PldaUnsupervisedAdaptor:

Public Member Functions
	PldaUnsupervisedAdaptor ()
void	AddStats (double weight, const Vector< double > &ivector)
void	AddStats (double weight, const Vector< float > &ivector)
void	UpdatePlda (const PldaUnsupervisedAdaptorConfig &config, Plda *plda) const

Private Attributes
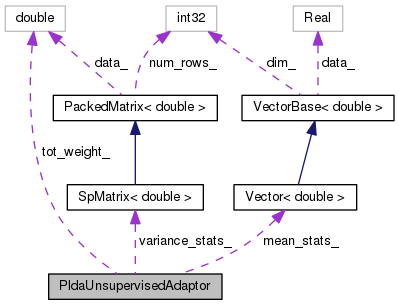
double	tot_weight_
Vector< double >	mean_stats_
SpMatrix< double >	variance_stats_

Detailed Description

This class takes unlabeled iVectors from the domain of interest and uses their mean and variance to adapt your PLDA matrices to a new domain.

This class also stores stats for this form of adaptation.

Definition at line 319 of file plda.h.

Constructor & Destructor Documentation

PldaUnsupervisedAdaptor()

PldaUnsupervisedAdaptor ( )

inline

Definition at line 321 of file plda.h.

: tot_weight_(0.0) { }

Member Function Documentation

AddStats() [1/2]

void AddStats	(	double	weight,
		const Vector< double > &	ivector
	)

Definition at line 595 of file plda.cc.

References VectorBase< Real >::Dim(), and KALDI_ASSERT.

Referenced by main().

                                                                      {
  if (mean_stats_.Dim() == 0) {
    mean_stats_.Resize(ivector.Dim());
    variance_stats_.Resize(ivector.Dim());
  }
  KALDI_ASSERT(weight >= 0.0);
  tot_weight_ += weight;
  mean_stats_.AddVec(weight, ivector);
  variance_stats_.AddVec2(weight, ivector);
}

AddStats() [2/2]

void AddStats	(	double	weight,
		const Vector< float > &	ivector
	)

Definition at line 607 of file plda.cc.

                                                                     {
  Vector<double> ivector_dbl(ivector);
  this->AddStats(weight, ivector_dbl);
}

UpdatePlda()

void UpdatePlda	(	const PldaUnsupervisedAdaptorConfig &	config,
		Plda *	plda
	)		const

Definition at line 613 of file plda.cc.

References SpMatrix< Real >::AddMat2Sp(), MatrixBase< Real >::AddMatMat(), MatrixBase< Real >::AddMatTp(), SpMatrix< Real >::AddTp2Sp(), VectorBase< Real >::AddVec(), SpMatrix< Real >::AddVec2(), PldaUnsupervisedAdaptorConfig::between_covar_scale, TpMatrix< Real >::Cholesky(), MatrixBase< Real >::CopyFromMat(), VectorBase< Real >::CopyFromVec(), Plda::Dim(), SpMatrix< Real >::Eig(), rnnlm::i, TpMatrix< Real >::Invert(), MatrixBase< Real >::Invert(), KALDI_ASSERT, KALDI_LOG, kaldi::kNoTrans, kaldi::kTrans, Plda::mean_, PldaUnsupervisedAdaptorConfig::mean_diff_scale, Plda::psi_, MatrixBase< Real >::Row(), PackedMatrix< Real >::Scale(), kaldi::SortSvd(), Plda::transform_, and PldaUnsupervisedAdaptorConfig::within_covar_scale.

Referenced by main().

                                                           {
  KALDI_ASSERT(tot_weight_ > 0.0);
  int32 dim = mean_stats_.Dim();
  KALDI_ASSERT(dim == plda->Dim());
  Vector<double> mean(mean_stats_);
  mean.Scale(1.0 / tot_weight_);
  SpMatrix<double> variance(variance_stats_);
  variance.Scale(1.0 / tot_weight_);
  variance.AddVec2(-1.0, mean);  // Make it the uncentered variance.

  // mean_diff of the adaptation data from the training data.  We optionally add
  // this to our total covariance matrix
  Vector<double> mean_diff(mean);
  mean_diff.AddVec(-1.0, plda->mean_);
  KALDI_ASSERT(config.mean_diff_scale >= 0.0);
  variance.AddVec2(config.mean_diff_scale, mean_diff);

  // update the plda's mean data-member with our adaptation-data mean.
  plda->mean_.CopyFromVec(mean);


  // transform_model_ is a row-scaled version of plda->transform_ that
  // transforms into the space where the total covariance is 1.0.  Because
  // plda->transform_ transforms into a space where the within-class covar is
  // 1.0 and the the between-class covar is diag(plda->psi_), we need to scale
  // each dimension i by 1.0 / sqrt(1.0 + plda->psi_(i))

  Matrix<double> transform_mod(plda->transform_);
  for (int32 i = 0; i < dim; i++)
    transform_mod.Row(i).Scale(1.0 / sqrt(1.0 + plda->psi_(i)));

  // project the variance of the adaptation set into this space where
  // the total covariance is unit.
  SpMatrix<double> variance_proj(dim);
  variance_proj.AddMat2Sp(1.0, transform_mod, kNoTrans,
                          variance, 0.0);

  // Do eigenvalue decomposition of variance_proj; this will tell us the
  // directions in which the adaptation-data covariance is more than
  // the training-data covariance.
  Matrix<double> P(dim, dim);
  Vector<double> s(dim);
  variance_proj.Eig(&s, &P);
  SortSvd(&s, &P);
  KALDI_LOG << "Eigenvalues of adaptation-data total-covariance in space where "
            << "training-data total-covariance is unit, is: " << s;

  // W, B are the (within,between)-class covars in the space transformed by
  // transform_mod.
  SpMatrix<double> W(dim), B(dim);
  for (int32 i = 0; i < dim; i++) {
    W(i, i) =           1.0 / (1.0 + plda->psi_(i)),
    B(i, i) = plda->psi_(i) / (1.0 + plda->psi_(i));
  }

  // OK, so variance_proj (projected by transform_mod) is P diag(s) P^T.
  // Suppose that after transform_mod we project by P^T.  Then the adaptation-data's
  // variance would be P^T P diag(s) P^T P = diag(s), and the PLDA model's
  // within class variance would be P^T W P and its between-class variance would be
  // P^T B P.  We'd still have that W+B = I in this space.
  // First let's compute these projected variances... we call the "proj2" because
  // it's after the data has been projected twice (actually, transformed, as there is no
  // dimension loss), by transform_mod and then P^T.

  SpMatrix<double> Wproj2(dim), Bproj2(dim);
  Wproj2.AddMat2Sp(1.0, P, kTrans, W, 0.0);
  Bproj2.AddMat2Sp(1.0, P, kTrans, B, 0.0);

  Matrix<double> Ptrans(P, kTrans);

  SpMatrix<double> Wproj2mod(Wproj2), Bproj2mod(Bproj2);

  for (int32 i = 0; i < dim; i++) {
    // For this eigenvalue, compute the within-class covar projected with this direction,
    // and the same for between.
    BaseFloat within = Wproj2(i, i),
        between = Bproj2(i, i);
    KALDI_LOG << "For " << i << "'th eigenvalue, value is " << s(i)
              << ", within-class covar in this direction is " << within
              << ", between-class is " << between;
    if (s(i) > 1.0) {
      double excess_eig = s(i) - 1.0;
      double excess_within_covar = excess_eig * config.within_covar_scale,
          excess_between_covar = excess_eig * config.between_covar_scale;
      Wproj2mod(i, i) += excess_within_covar;
      Bproj2mod(i, i) += excess_between_covar;
    } /*
        Below I was considering a method like below, to try to scale up
        the dimensions that had less variance than expected in our sample..
        this didn't help, and actually when I set that power to +0.2 instead
        of -0.5 it gave me an improvement on sre08.  But I'm not sure
        about this.. it just doesn't seem right.
      else {
      BaseFloat scale = pow(std::max(1.0e-10, s(i)), -0.5);
      BaseFloat max_scale = 10.0;  // I'll make this configurable later.
      scale = std::min(scale, max_scale);
      Ptrans.Row(i).Scale(scale);
      } */
  }

  // combined transform "transform_mod" and then P^T that takes us to the space
  // where {W,B}proj2{,mod} are.
  Matrix<double> combined_trans(dim, dim);
  combined_trans.AddMatMat(1.0, Ptrans, kNoTrans,
                           transform_mod, kNoTrans, 0.0);
  Matrix<double> combined_trans_inv(combined_trans);  // ... and its inverse.
  combined_trans_inv.Invert();

  // Wmod and Bmod are as Wproj2 and Bproj2 but taken back into the original
  // iVector space.
  SpMatrix<double> Wmod(dim), Bmod(dim);
  Wmod.AddMat2Sp(1.0, combined_trans_inv, kNoTrans, Wproj2mod, 0.0);
  Bmod.AddMat2Sp(1.0, combined_trans_inv, kNoTrans, Bproj2mod, 0.0);

  TpMatrix<double> C(dim);
  // Do Cholesky Wmod = C C^T.  Now if we use C^{-1} as a transform, we have
  // C^{-1} W C^{-T} = I, so it makes the within-class covar unit.
  C.Cholesky(Wmod);
  TpMatrix<double> Cinv(C);
  Cinv.Invert();

  // Bmod_proj is Bmod projected by Cinv.
  SpMatrix<double> Bmod_proj(dim);
  Bmod_proj.AddTp2Sp(1.0, Cinv, kNoTrans, Bmod, 0.0);
  Vector<double> psi_new(dim);
  Matrix<double> Q(dim, dim);
  // Do symmetric eigenvalue decomposition of Bmod_proj, so
  // Bmod_proj = Q diag(psi_new) Q^T
  Bmod_proj.Eig(&psi_new, &Q);
  SortSvd(&psi_new, &Q);
  // This means that if we use Q^T as a transform, then Q^T Bmod_proj Q =
  // diag(psi_new), hence Q^T diagonalizes Bmod_proj (while leaving the
  // within-covar unit).
  // The final transform we want, that projects from our original
  // space to our newly normalized space, is:
  // first Cinv, then Q^T, i.e. the
  // matrix Q^T Cinv.
  Matrix<double> final_transform(dim, dim);
  final_transform.AddMatTp(1.0, Q, kTrans, Cinv, kNoTrans, 0.0);

  KALDI_LOG << "Old diagonal of between-class covar was: "
            << plda->psi_ << ", new diagonal is "
            << psi_new;
  plda->transform_.CopyFromMat(final_transform);
  plda->psi_.CopyFromVec(psi_new);
}

Member Data Documentation

mean_stats_

Vector<double> mean_stats_

private

Definition at line 332 of file plda.h.

tot_weight_

double tot_weight_

private

Definition at line 331 of file plda.h.

variance_stats_

SpMatrix<double> variance_stats_

private

Definition at line 333 of file plda.h.

---

The documentation for this class was generated from the following files:

• ivector/plda.h
• ivector/plda.cc