 |
|
This documentation covers Dan Povey's version of the deep neural network code in Kaldi. For an overview of all deep neural network code in Kaldi, see Deep Neural Networks in Kaldi, and for Karel's version, see Karel's DNN implementation.
This (rather hastily prepared) introduction to the DNN setup includes Looking at the scripts, Use of GPUs or CPUs, Tuning the neural network training and dnn2_preconditioning.
The first place to look to get a top level overview of the neural net training is probably the scripts. In the standard example scripts in egs/rm/s5, egs/wsj/s5 and egs/swbd/s5b, the top-level script is run.sh. This script calls (sometimes commented out) a script called local/run_nnet2.sh. This is the top-level example script for Dan's setup. In local/run_nnet2.sh, there are a few different examples demonstrating different recipes, and we try to indicate which one we consider to be the "primary" recipe at any point in time. Rather than just running local/run_nnet2.sh, which might take some time, we suggest that you just run the "primary" one. This is generally a p-norm network (see this paper ).
Note: the previous top-level training script, which used to be steps/nnet2/train_pnorm.sh, has now been deprecated and you should use steps/nnet2/train_pnorm_fast.sh. This script is going to parallelize the training over multiple nodes, in a way we'll explain below.
The input features to the neural network are configurable to some extent, but by default they consist of the same fully processed, adapted features that are fed in to a GMM-based model in speech recognition: usually MFCC(spliced)+LDA+MLLT+fMLLR, 40-dimensional features. The network sees a window of these features, with 4 frames on each side of the central frame by default. Because it is hard for neural networks to learn from correlated input, we will multiply these (40 * 7)-dimensional features by a fixed transform that decorrelates the features. Creating this transform is the first thing the training script does; it is accomplished by a call to steps/nnet2/get_lda.sh. This was originally based on our work in this paper , but the transform that the code currently computes is not exactly LDA: in the default case it's more like a non-dimension-reducing form of the LDA transform, followed by a reduction of the variance of dimensions of the output feature in which the between-class variance is low. (This is unpublished; see the code). The other type of feature that the scripts support is un-processed features, e.g. MFCC features; this can be activated via the –feat-type option that must be passed in to the get_egs.sh and get_lda.sh scripts vis the –egs-opts and –lda-opts options.
Note that to search for options in scripts, the best way is to just search for the option name with internal dashes replaced with underscores: in this case, for feat_type, egs_opts, and lda_opts. The script utils/parse_options.sh automatically interprets command line arguments as setting the corresponding variables.
Suppose that the top-level script (e.g. steps/nnet2/train_pnorm.sh) is creating a model in exp/nnet5d/. The first thing this script does is to call steps/nnet2/get_egs.sh. This puts quite a lot of data in exp/nnet5d/egs/. This relates to frame-level randomization of the input, which is needed for Stochastic Gradient Descent training. We do the randomization just once, so that during the actual training we can access the data sequentially. This means that, every epoch, we acccess the data in essentially the same order; this means that the disk access is sequential which is kinder to the disk and the network. (Actually we do randomization using a small buffer using a different seed each iterations, but this will only change the order locally).
If you look in (for example) exp/nnet5d/egs/ you will see a lot of files called egs.1.1.ark, egs.1.2.ark, and so on. These are archives containing many instances of a class called NnetTrainingExample. This class contains the label information for a single frame, and a sufficient temporal window of the feature input (typically 40-dimensional) to be able to do the neural net computation for that frame. Rather than doing the frame-splicing externally to the neural network, the neural net training code has a concept of time and "knows" how much temporal context it needs (see the functions RightContext() and LeftContext()). The two integer indices in the filenames are the job-index and the iteration index. The job-index corresponds to which parallel job we are. For instance, if we're running using CPUs, using 16 machines in parallel (each machine with some number of threads that's irrelevant here), then the job-index would range from 1 to 16, or if we're using GPUs, say 8 GPUs in parallel, then the job-index would range from 1 to 8. The extent of the iteration index depends how much data we have. We aim for each archive to have, by default, around 200,000 samples in it. The number of iteration indices will be determined by how much data we have and how many jobs there are. We'll be running training for many epochs (e.g. 20), and each epoch we'll do that many iterations (it could be 1 for a small database like Resource Management, or many tens for larger databases).
The directory (e.g.) exp/nnet5d/egs/ will contain a few other files: iters_per_epoch, num_jobs_nnet and sample_per_iter contain some numbers as discussed above; in one Resource Management example these are 1, 16 and 85493 respectively. It also contains valid_diagnostic.egs, which is a small archive of examples taken from held-out utterances which is used for diagnostics (see e.g. exp/nnet5d/log/compute_prob_valid.*.log), and train_diagnostic.egs, which is as valid_diagnostic.egs except not held-out; see exp/nnet5d/log/compute_prob_valid.*.log for diagnostics derived from this. The file combine.egs is a slightly larger subset of training data which is used for computing combination weights of neural net parameters at the end of training.
We initialize the neural net with a single hidden layer; we will increase the number of hidden layers later in training, to a configurable number (usually in the range 2 to 5). The script creates a configuration file named something like exp/nnet4d/nnet.config. This is passed to a program called nnet-am-init which creates the initial model. An example configuration file from the p-norm setup for Resource Management looks like this
SpliceComponent input-dim=40 left-context=4 right-context=4 const-component-dim=0 FixedAffineComponent matrix=exp/nnet4d/lda.mat AffineComponentPreconditionedOnline input-dim=360 output-dim=1000 alpha=4.0 num-samples-history=2000 update-period=4 rank-in=20 rank-out=80 max-change-per-sample=0.075 learning-rate=0.02 param-stddev=0.0316227766016838 bias-stddev=0.5 PnormComponent input-dim=1000 output-dim=200 p=2 NormalizeComponent dim=200 AffineComponentPreconditionedOnline input-dim=200 output-dim=1475 alpha=4.0 num-samples-history=2000 update-period=4 rank-in=20 rank-out=80 max-change-per-sample=0.075 learning-rate=0.02 param-stddev=0 bias-stddev=0 SoftmaxComponent dim=1475
The FixedAffineComponent is the LDA-like decorrelating transform that we mentioned earlier. The AffineComponentPreconditionedOnline is a refinement of AffineComponent. An AffineComponent would consist of the standard (weight matrix plus bias term) that appears in neural networks, trained with standard stochastic gradient descent. AffineComponentPreconditionedOnline is as AffineComponent, but the training procedure uses not just a single global learning rate but a matrix-valued learning rate to precondition the gradient descent. We aim to describe more about this below (see dnn2_preconditioning). The PnormComponent is the nonlinearity; for a more conventional neural network this would be TanhComponent instead. The NormalizeComponent is something we add to stabilize the training of p-norm networks. It is also a fixed, non-trainable nonlinearity, but it acts not on individual activations but on the whole vector of them (for a single frame), to renormalize them to have unit standard deviation. The SoftmaxComponent is the final nonlinearity that produces properly normalized probabilities at the output.
The script also produces a file called hidden.config which corresponds to what we add when we introduce a new hidden layer; in this example it looks like this:
AffineComponentPreconditionedOnline input-dim=200 output-dim=1000 alpha=4.0 num-samples-history=2000 update-period=4 rank-in=20 rank-out=80 max-change-per-sample=0.075 learning-rate=0.02 param-stddev=0.0316227766016838 bias-stddev=0.5 PnormComponent input-dim=1000 output-dim=200 p=2 NormalizeComponent dim=200
This won't be used until after the first couple of iterations of training.
The next small step that the script does is to call nnet-train-transitions. This computes the transition probabilities that will be used in the HMMs in decoding (which has nothing to do with the neural net itself), and also computes the prior probabilities of the "targets" (the several thousand context-dependent states). Later, when we do decoding, we will divide the posteriors computed by the network by these priors to get "pseudo-likelihoods"; these are more compatible with the HMM framework than raw posteriors.
Next we come to the main training phase. This is a loop over an iteration counter x, which ranges from 0 to num_iters - 1. The number of iterations num_iters is the number of epochs we train for times the number of iterations per epoch. The number of epochs we train for is the sum of num_epochs (default: 15) plus num_epochs_extra (default: 5). This has to do with the learning rate schedule: by default, we decrease the learning rate from initial_learning_rate (default: 0.04) to final_learning_rate (default: 0.004) for 15 epochs and then leave it constant at final_learning rate for 5 epochs. The number of iterations per epoch is stored in a file like egs/nnet5d/egs/iters_per_epoch; it depends how much data we have and how many training jobs we run in parallel, and can vary from one to many tens.
On each iteration, the first thing we do is compute some diagnostics: the objective functions on training and validation data (for iteration 10, see for example egs/nnet5d/log/compute_prob_valid.10.log and egs/nnet5d/log/compute_prob_train.10.log). In a file like egs/nnet5d/log/progress.10.log you will see diagnostics that show much the parameters of each layer are changing, and how much of the change in training-data objective function can be attributed to the changes in each layer.
Below is an example of looking at these diagnostics in one particular directory:
grep LOG exp/nnet4d/log/compute_prob_*.10.log exp/nnet4d/log/compute_prob_train.10.log:LOG<snip> Saw 4000 examples, average probability is -0.894922 and accuracy is 0.729 with total weight 4000 exp/nnet4d/log/compute_prob_valid.10.log:LOG<snip> Saw 4000 examples, average probability is -1.16311 and accuracy is 0.6585 with total weight 4000
You can see that the training set objective function is better, at -0.89, than the validation set objective function, at -1.16. This is a cross-entropy, also known as the average log-probability per frame of the correct class. It's normal for the training and validation objective functions to differ quite a lot because neural networks have a high learning capacity: for well-tuned systems on only a few hours of data, they can differ by as much as a factor of two (but much less when you have more training data). If you add more parameters the training objective function will always improve but the validation objective function may degrade. However, tuning based on the validation set objective function is generally not a good idea as it will tend to lead you towards systems that have too few parameters. It can be better for Word Error Rates to add parameters even if it degrades the validation set performance to some extent.
In a file such as exp/nnet4d/log/progress.10.log you'll find some other diagnostics that look like the following:
LOG <snip> Total diff per component is [ 0.00133411 0.0020857 0.00218908 ] LOG <snip> Parameter differences per layer are [ 0.925833 1.03782 0.877185 ] LOG <snip> Relative parameter differences per layer are [ 0.016644 0.0175719 0.00496279 ]
The top line regarding "Total diff per component" breaks down the change in training-set objective function by the contribution of different layers, and the other lines say how large the parameter change was for the different layers.
The logs of the main training job can be found (for example) in exp/nnet5a/log/train.*.*.log. The first index is the iteration number and the second index is the one of, say, 4 or 16 parallel jobs that we run (this number is the –num-jobs-nnet parameter to the script). Below is an example of one of the training jobs:
#> cat exp/nnet4d/log/train.10.1.log # Running on a11 # Started at Sat Mar 15 16:32:08 EDT 2014 # nnet-shuffle-egs --buffer-size=5000 --srand=10 ark:exp/nnet4d/egs/egs.1.0.ark ark:- | \ nnet-train-parallel --num-threads=16 --minibatch-size=128 --srand=10 exp/nnet4d/10.mdl \ <snip> LOG (nnet-shuffle-egs:main():nnet-shuffle-egs.cc:100) Shuffled order of 79100 neural-network \ training examples using a buffer (partial randomization) LOG (nnet-train-parallel:DoBackpropParallel():nnet-update-parallel.cc:256) Did backprop on \ 79100 examples, average log-prob per frame is -1.4309 LOG (nnet-train-parallel:main():nnet-train-parallel.cc:104) Finished training, processed \ 79100 training examples (weighted). Wrote model to exp/nnet4d/11.1.mdl # Accounting: time=18 threads=16 # Finished at Sat Mar 15 16:32:26 EDT 2014 with status 0
This particular job was run without a GPU, using 16 CPU threads in parallel, and only took 18 seconds to complete. The main job that is running here is nnet-train-parallel, which is essentially doing Stochastic Gradient Descent, parallelized with something similar to Hogwild! (i.e. without locks), with a minibatch size of 128 per thread. The model is output to 11.1.mdl. In exp/nnet4d/log/average.10.log you will see the log output for a program called nnet-am-average that averages all the SGD-trained models for this iteration. It also modifies the learning rates as dictated by our learning rate schedule, which is exponentially decreasing (see the paper "An Empirical study of learning rates in deep neural networks for speech recognition" by Andrew Senior et. al., which found that this works well for speech recognition). Note: it is our practice in the tanh recipes to use a halved learning rate for the last two layers; see the option –final-learning-rate-factor to the script train_tanh.sh.
The basic parallelization method is to train with Stochastic Gradient Descent for a few hundred thousand samples, using different data in different jobs and then to average the models. Since the objective function is not convex in the parameters, it may seem surprising that this works, but empirically convexity does not seem to be an issue here. Note: it seems to be important that we are doing the "preconditioned update" which we describe below; we have experiments that indicate this is important for the success of our parallization method. Also note that in the more recent training scripts (train_norm_fast.sh and train_tanh_fast.sh), we don't do the parallelization and averaging on iterations where we've either just initialized the model or just added a new layer. This is because we found that under those circumstances, sometimes the averaging can fail to be helpful due to lack of convexity (i.e., the objective function given the averaged model is worse than the average of the individual objective functions).
If you look in, for example, exp/nnet4d/log/combine.log, you will see how the final neural network called "final.mdl" is created. This is based on combining the parameters of the models created on the final N iterations, where N corresponds to the argument –num-iters-final to the script (default: 20). The basic idea is that we can reduce the variance of the estimate by averaging over a number of iterations. We can't easily prove that this would be better than just taking the final model (because it's not a convex problem), but in practice it is. Actually, "combine.log" isn't just taking the average of the parameters. It's using a subset of training-data examples (taken from exp/nnet4d/egs/combine.egs, in this case) to optimize a set of weights, which are not constrained to be positive. The objective function is the normal objective function (log-probability) on that subset, and the optimization method is L-BFGS, with a special preconditioning method that we won't go into here. There are separate weights for each component and each iteration, so in this case we are learning (20 * 3 = 60) weights. In the original version of this method, we used validation data to estimate the paraemters, but we found that it works best when using a random subset of training data for this purpose.
#> cat exp/nnet4d/log/combine.log
<snip>
Scale parameters are [
-0.109349 -0.365521 -0.760345
0.124764 -0.142875 -1.02651
0.117608 0.334453 -0.762045
-0.186654 -0.286753 -0.522608
-0.697463 0.0842729 -0.274787
-0.0995975 -0.102453 -0.154562
-0.141524 -0.445594 -0.134846
-0.429088 -1.86144 -0.165885
0.152729 0.380491 0.212379
0.178501 -0.0663124 0.183646
0.111049 0.223023 0.51741
0.34404 0.437391 0.666507
0.710299 0.737166 1.0455
0.859282 1.9126 1.97164 ]
LOG <snip> Combining nnets, objf per frame changed from -1.05681 to -0.989872
LOG <snip> Finished combining neural nets, wrote model to exp/nnet4a2/final.mdl
The combination weights are printed out as a matrix where the row-index corresponds to the iteration and the column-index corresponds to the layer. You can see that the combination weights are positive for later iterations and negative for earlier ones, which we can interpret as an attempt to take the model further in the dirction that it was already going. We use the training data rather than the validation data for this because we found this works better, although probably using validation data would be more natural; we think the reason might relate to a bad interaction the "dividing-by-the prior" normalization that is done for speech recognition.
If use use the nnet-am-info program to print information about exp/nnet4d/final.mdl, you'll see that there is a layer of size 4000 just before the output layer, which is of size 1483 because the decision tree had 1483 leaves:
#> nnet-am-info exp/nnet4d/final.mdl num-components 11 num-updatable-components 3 left-context 4 right-context 4 input-dim 40 output-dim 1483 parameter-dim 1366000 component 0 : SpliceComponent, input-dim=40, output-dim=360, context=4/4 component 1 : FixedAffineComponent, input-dim=360, output-dim=360, linear-params-stddev=0.0386901, bias-params-stddev=0.0315842 component 2 : AffineComponentPreconditioned, input-dim=360, output-dim=1000, linear-params-stddev=0.988958, bias-params-stddev=2.98569, learning-rate=0.004, alpha=4, max-change=10 component 3 : PnormComponent, input-dim = 1000, output-dim = 200, p = 2 component 4 : NormalizeComponent, input-dim=200, output-dim=200 component 5 : AffineComponentPreconditioned, input-dim=200, output-dim=1000, linear-params-stddev=0.998705, bias-params-stddev=1.23249, learning-rate=0.004, alpha=4, max-change=10 component 6 : PnormComponent, input-dim = 1000, output-dim = 200, p = 2 component 7 : NormalizeComponent, input-dim=200, output-dim=200 component 8 : AffineComponentPreconditioned, input-dim=200, output-dim=4000, linear-params-stddev=0.719869, bias-params-stddev=1.69202, learning-rate=0.004, alpha=4, max-change=10 component 9 : SoftmaxComponent, input-dim=4000, output-dim=4000 component 10 : SumGroupComponent, input-dim=4000, output-dim=1483 prior dimension: 1483, prior sum: 1, prior min: 7.96841e-05 LOG (nnet-am-info:main():nnet-am-info.cc:60) Printed info about baseline/exp/nnet4d/final.mdl
The softmax goes to dimension 4000 and this is then reduced to 1483 by something called SumGroupComponent. You can find a little more about this using the command nnet-am-copy to convert it to text format:
#> nnet-am-copy --binary=false baseline/exp/nnet4d/final.mdl - | grep SumGroup nnet-am-copy --binary=false baseline/exp/nnet4d/final.mdl - <SumGroupComponent> <Sizes> [ 6 3 3 3 2 3 3 3 2 3 2 2 3 3 3 3 2 3 3 3 3 \ 3 3 4 2 1 2 3 3 3 2 2 2 3 2 2 3 3 3 3 2 4 2 3 2 3 3 3 4 2 2 3 3 2 4 3 3 \ <snip> 4 3 3 2 3 3 2 2 2 3 3 3 3 3 1 2 3 1 3 2 ]
What is happening is that the softmax component produces a larger number of posteriors than we need (4000 instead of 1483) and small groups of those posteriors (ranging in size betwen 1 and 6 in this example) are summed up to produce the output of dimension 1483. We call it "mixing up" by analogy with the process that is done in training of Gaussian Mixture Models for speech recognition, whereby we split Gaussians into two and perturb the means. In this case we split rows of the final weight matrix in two and perturb them. These extra targets get added about halfway through training. The relevant log file is below:
cat exp/nnet4d/log/mix_up.31.log # Running on a11 # Started at Sat Mar 15 15:00:23 EDT 2014 # nnet-am-mixup --min-count=10 --num-mixtures=4000 exp/nnet4d/32.mdl exp/nnet4d/32.mdl nnet-am-mixup --min-count=10 --num-mixtures=4000 exp/nnet4d/32.mdl exp/nnet4d/32.mdl LOG (nnet-am-mixup:GiveNnetCorrectTopology():mixup-nnet.cc:46) Adding SumGroupComponent to neural net. LOG (nnet-am-mixup:MixUp():mixup-nnet.cc:214) Mixed up from dimension of 1483 to 4000 in the softmax layer. LOG (nnet-am-mixup:main():nnet-am-mixup.cc:77) Mixed up neural net from exp/nnet4d/32.mdl and wrote it to exp/nnet4d/32.mdl # Accounting: time=0 threads=1 # Finished at Sat Mar 15 15:00:23 EDT 2014 with status 0
"Shrinking" and "fixing" are processes that we don't actually use for the p-norm network that we are using as our primary example, but they are relevant for neural networks that were trained using the script steps/nnet2/train_tanh.sh, or more generally any network that has sigmoidal activations. What we are trying to address is the pathology that occurs with these type of activations, that neurons become "over-saturated" on too much of the training data (meaning, it gets outside the part of the activation that has a substantial slope) and training becomes very slow.
Let's look at one of the logs, for shrinking, first:
#> cat exp/nnet4c/log/shrink.10.log # Running on a14 # Started at Sat Mar 15 14:25:43 EDT 2014 # nnet-subset-egs --n=2000 --randomize-order=true --srand=10 ark:exp/nnet4c/egs/train_diagnostic.egs ark:- | \ nnet-combine-fast --use-gpu=no --num-threads=16 --verbose=3 --minibatch-size=125 exp/nnet4c/11.mdl \ ark:- exp/nnet4c/11.mdl <snip> LOG <snip> Scale parameters are [ 0.976785 1.044 1.1043 ] LOG <snip> Combining nnets, objf per frame changed from -1.01129 to -1.00195 LOG <snip> Finished combining neural nets, wrote model to exp/nnet4c/11.mdl
It is using nnet-combine-fast, but just giving it one neural net as input, so the only thing it can optimize is the scales of the parameters at the various layers of the network. These scales are all quite close to one, and some are greater than one, so perhaps shrinking* is a misnomer in this case. We have found cases where this "shrinking" is quite helpful, but probably in this case it isn't making much difference.
Next, look at a log for "fixing"; this is done on every iteration when we don't do "shrinking":
#> cat exp/nnet4c/log/fix.1.log nnet-am-fix exp/nnet4c/2.mdl exp/nnet4c/2.mdl LOG (nnet-am-fix:FixNnet():nnet-fix.cc:94) For layer 2, decreased parameters for 0 indexes, \ and increased them for 0 out of a total of 375 LOG (nnet-am-fix:FixNnet():nnet-fix.cc:94) For layer 4, decreased parameters for 1 indexes, \ and increased them for 0 out of a total of 375 LOG (nnet-am-fix:main():nnet-am-fix.cc:82) Copied neural net from exp/nnet4c/2.mdl to exp/nnet4c/2.mdl
What this is doing is looking at the average of the derivative of the tanh activation function, measured over the training data. For tanh, this derivative cannot exceed 1.0 for any data point. If, for a particular neuron, its average is very much smaller than this (we use a threshold of 0.1 by default), then it means we are oversaturated and we decrease the weights and the bias at the input of that neuron by a factor of up to 2 to compensate. As you can see in the log, this only happened for one neuron on this iteration, indicating that it wasn't much of a problem for this particular run (it will tend to happen more often if we use higher learning rates).
The setup makes it possible to fairly transparently train with either GPUs or CPUs. Note that if you want to run with GPUs then it has to be compiled with GPU support. That means that in src/, you have to run "configure" and "make" on a machine that has the NVidia CUDA toolkit (that is, a machine on which the command "nvcc" can be executed). If Kaldi is compiled with GPU support, then the neural net training binaries will be able to train with GPU. You can tell whether Kaldi has been compiled for GPU by using the command "ldd" on a program which would use the GPU, and checking if libcublas is compiled in, e.g.:
src#> ldd nnet2bin/nnet-train-simple | grep cu libcublas.so.4 => /home/dpovey/libs/libcublas.so.4 (0x00007f1fa135e000) libcudart.so.4 => /home/dpovey/libs/libcudart.so.4 (0x00007f1fa1100000)
You will know when the training is using a GPU because you will see things like this in the files train.*.*.log:
LOG (nnet-train-simple:IsComputeExclusive():cu-device.cc:209) CUDA setup operating \
under Compute Exclusive Mode.
LOG (nnet-train-simple:FinalizeActiveGpu():cu-device.cc:174) The active GPU is [0]: \
Tesla K10.G2.8GB free:3516M, used:66M, total:3583M, free/total:0.981389 version 3.0
Some of the command-line programs take an option –use-gpu which takes the values "yes", "no" or "optional", and directs it whether to use a GPU (if set to "optional", it will use the GPU only if one is available). But actually we don't use this mechanism in the scripts much because we have two different binaries for GPU versus CPU training. The CPU version is nnet-train-parallel, and it is so called because it supports multiple threads. We typically use 16 threads when using a CPU. This is doing multi-core stochastic gradient descent without any locking, which we can probably view as a form of Hogwild!. Incidentally, when doing this multi-threaded update it is not advisable to let the minibatch size increase above 128 or so, because this can lead to instability. We consider that "effective minibatch size" as equal to the minibatch size times the number of threads, and if this gets too large the updates can diverge. Note that we have formulated the stochastic gradient descent so that the gradients get summed over the members of the minibatch, not averaged. Also note that the only reason why we can't just use nnet-train-parallel with one thread for GPU-based training is that nnet-train-parallel uses two threads even if configured with –num-threads=1 (because one thread is dedicated to I/O), and CUDA does not work easily with multi-threaded programs because the GPU context is tied to a single thread.
If you want to switch between using CPU and GPU when invoking scripts like train_tanh.sh and train_pnorm.sh, there are a few separate things you have to change when invoking the script (this is probably not ideal). These programs have an options –parallel-opts, which consists of the extra flags that are passed to queue.pl (or some similar script). Here we assume queue.pl is invoking GridEngine and the arguments will get passed to GridEngine. The default value of –parallel-opts is to run using a CPU with 16 threads, and this is "-pe smp 16 -l ram_free=1G,mem_free=1G". This only affects what resources we request from the queue, and does not affect what the script actually runs; we'll have to separately tell the script to actually use 16 threads, via the –num-threads option (the default is 16). The option "ram_free=1G" is probably not relevant to all queues as it is a resource that we added manually to our queue to account for memory use; you can just remove it if there is no such resource at your location. The default setup uses CPU with 16 threads; if you want to use a GPU you have to invoke the script with options like
--num-threads 1 --parallel-opts "-l gpu=1"
Again, we emphasize that this "gpu=1" resource just reflects the way we invoke GPUs in one particular cluster, and other clusters may be different because the concept of a GPU is not baked into GridEngine– queues may be configured by the administrator in different ways. Basically the string needs to be whatever options you need to give to "qstat" so that it will request a GPU. If all this is just running on a single machine without GridEngine and you are just using run.pl to launch jobs, then parallel-opts can just be the empty string. If you invoke the script with –num-threads=1 then it will call nnet-train-simple, which by default if compiled for GPUs will try to use a GPU. If –num-threads exceeds one it will call nnet-train-parallel, which does not use a GPU.
What we described above describes the key point of how to switch between CPU and GPU training. You might notice that in some of the example scripts (e.g. comparing a pair of scripts like local/nnet2/run_4c.sh and local/nnet2/run_4c_gpu.sh), the value of the –num-jobs-nnet option is different between the GPU and CPU versions of the script, e.g. it might be 8 for the CPU version and 4 for the GPU version. Also the –minibatch-size sometimes differs between the two versions, being for example 512 for the GPU setup and 128 for the CPU-based setup, and the learning rates sometimes differ too.
Here will explain the reason for those differences. Firstly, regarding the minibatch size. You should know that our SGD is formulated so that the gradient is summed not averaged over the minibatch; in our opinion this minimizes the need to change the learning rate when the minibatch size changes. Generally speaking, the matrix multiplications will be fastest (per sample) with a largish minibatch size such as 512. Also the preconditioning method that we use, which we describe below in Preconditioned Stochastic Gradient Descent, works better with larger minibatch size so the training actually converges a little faster with a larger minibatch size such as 512 or even 1024. However, there is a limit to how large the minibatch size can be that relates to instability of the SGD update (with parameters seesawing back and forth uncontrollably). If the minibatch size is too large the update can become unstable. Once the instability gets too large it gets limited by our –max-change option, which affects how much we allow the parameters to change for each minibatch, so it won't generally cause the training-set probabilities to go all the way to -infinity, but they may drop considerably. If you see in compute_prob_train.*.log an objective function below the negative natural log of the number of leaves in your system (typically -7 or so, you'll see this value in compute_prob_train.0.log), it means the network is doing worse than chance, and this is generally because instability has set in. The solution is usually to decrease the learning rate or the minibatch size.
The relevance of this discussion about instability to the multi-threaded update is as follows. When we do the multi-threaded update, for the purposes of this instability it's as if the minibatch size is multiplied by the number of threads, so we have to keep the minibatch size lower than it would otherwise be. Generally we use 128 when training with multiple threads on the CPU. (We should mention, with regard to the multi-threaded CPU update, that we tried doing single-threaded training and allowing our BLAS implementation to use multiple threads, but we found that it was much faster to have separate threads doing SGD independently on the same parameters.)
Next, regarding the –num-jobs-nnet option: we sometimes use more (8 or 16) for the CPU-based setup, than for the GPU-based setup. The reason for this is simply that when testing the scripts we did not have as many GPUs as CPUs available. Also, the GPU training is generally a little faster than the CPU training– maybe 20% to 50% faster– so we felt that we could use fewer jobs to achieve the same total training time. But fundamentally the number of jobs is independent of whether we train on CPU or GPU.
The last change is the learning rate (the options –initial-learning-rate and –final-learning-rate), and this is related to the number of jobs (–num-jobs-nnet). Generally speaking, if we increase the number of jobs we also want to increase the learning rate by the same factor. Since the parallelization method is based on averaging the neural nets from parallel SGD runs, we view the "effective learning rate" per sample of the entire learning process as equal to the learning rate divided by the number of jobs. So when doubling the number of jobs, if we double the learning rate we keep the "effective learning rate" the same. But there is a limit to this. If the learning rate becomes too high it can lead to unstable, divergent updates with the parameters swinging back and forth. Therefore if the initial learning rate is getting too high we might be wary of increasing it too much. What "too high" means depends on the setup.
Generally speaking, when tuning the neural network training you should start from one of the example scripts invoked by one of the scripts in
egs/*/*/local/nnet2/
, and change the parameters in some way. We assume that you're running either train_tanh.sh and train_pnorm.sh.
One of the more important parameters to tune is the number of hidden layers (–num-hidden-layers). This should generally be between 2 and 5 for tanh networks (it should be more if there is more data) and maybe betweeen 2 and 3 or 4 for p-norm networks. When we change the number of hidden layers we generally leave the number of hidden nodes fixed (at 512, or 1024, or whatever).
You can also change the hidden layer dimension –hidden-layer-dim for tanh networks; this is the number of neurons in the hidden layers. Generally this should be more if there is more data, but bear in mind that the number of parameters grows almost quadratically as this increases, so you'll want to increase it with a power less than 0.5 as you add more data (e.g. if you have 10 times as much data, doubling the hidden layer size might make sense). We've never gone above 2048 or so. We consider 1024 hidden nodes to be a large network.
For the p-norm networks there is no –hidden-layer-dim parameter; instead there are two parameters, –pnorm-output-dim and –pnorm-input-dim. They default to (3000, 300) respectively. The input-dim needs to be an exact integer multiple of the output-dim; we normally use a ratio of 5 or 10. This affects the number of parameters; you will want more for larger datasets, but as with the hidden-layer size for the tanh networks, it should increase only gradually with the amount of data.
Another option that relates to the number of parameters is the –mix-up option. This is responsible for creating multiple "virtual" targets for each leaf, increasing the final softmax-layer size above the number of leaves in the decision tree (you can work out the number of leaves from doing am-info on the final.mdl in the input directory to the neural network training; it will usually be several thousand. The –mix-up parameter should generally be around twice the number of leaves, but generally the error rate is not that sensitive to it.
Another important tunable parameter is the learning rate. There are two main parameters: –initial-learning-rate and –final-learning-rate. The defaults are 0.04 and 0.004 respectively. We generally set these so that the final learning rate is about one fifth or one tenth of the initial learning reate. The default values of 0.04 and 0.004 are only suitable for small datasets, for example Resource Management, at three hours. If the dataset is larger you'll be training for longer, so it's not necessariy to have such a high learning rate. For hundreds of hours, a learning rate even ten times smaller than this may be suitable. Below we'll mention how the learning rate interacts with the number of jobs.
It can be hard to tell whether the learning rates are too low or too high without plotting a graph of objective function versus time. If the learning rate is too high you may get rapid initial improvement in the objective function followed by never getting a very good objective function value (as it's hindered by noisy gradients). But you also may get parameter oscillations, which will show up as very bad objective function values (this is particularly likely to happen if the minibatch size is large or you are using many threads). If the learning rate is too low, the objective function will improve more slowly and will take a long time to reach a plateau.
A learning rate parameter that you probably won't need to tune is the configuration value –final-learning-rate-factor in the train_tanh.sh script, which defaults to 0.5. This uses half the given learning rate, for the last two layers (i.e. the parameters just before the softmax and the last hidden layer). We introduced this parameter because we found that the last two layers seemed to learn much faster than the others and we wanted to balance them. The train_pnorm.sh script supports a similar configuration value –soft-max-learning-rate-factor, which affects just the parameters before the final softmax layer, but it defaults to 1.0.
Another tunable parameter is the minibatch size. We generally use a power of two for this, typically 128, 256 or 512. Generally a larger minibatch size is more efficient because it interacts well with optimizations used in matrix multiplication code, particularly on GPUs, but if it is too large (and if the learning rate is too high), it can lead to instability in the update. In the multi-threaded Hogwild! style update for CPU-based training, the update can be unstable if the minibatch size is too large. We generally use a minibatch size of 128 for multi-threaded CPU based training, and 512 for GPU-based training. This should not be necessary to tune further. We should mention, though, that the minibatch size interacts with the –max-change option which we discuss below, so that a larger minibatch size probably means the –max-change should be larger.
There is an option –max-change in the train_tanh.sh and train_pnorm.sh scripts that gets passed in to the initialization of the components that contain the weight matrices (these are of type AffineComponent or AffineComponentPreconditioned). The –max-change limits how much we allow the parameters to change per minibatch, measured in l2 norm, i.e. the matrix representing the change in parameters of any given layer, on any given minibatch, cannot exceed this value. Actually it happens that in order to do this as we stated above we would have to add a temporary matrix to store the change in parameters, and this is wasteful, so what we actually bound is the sum of the l2 norms of contributions of all the members of the minibatch. If this would exceed the "max-change", we multiply the learning rate used for that minibatch by a constant less than one to make sure it does not exceed the limit. If the max-change constraint is active, you will see message in the logs train.*.log that look like the following:
LOG <snip> Limiting step size to 40 using scaling factor 0.189877, for component index 8 LOG <snip> Limiting step size to 40 using scaling factor 0.188353, for component index 8
(actually this factor is smaller than normal– these factors that get printed out are normally much closer to one. Perhaps the learning rate was too high for this particular run. The –max-change is a kind of fail-safe mechanism to ensure that if the learning rate is too high (or the minibatch size too large), it can't lead to instability. The –max-change can slow down learning early on in training, particularly for the last layer or two; later in the training process the constraint should stop being active, and you should not see these messages in the logs towards the end of training. This parameter is not too critical. We usually set it to 40 if the minibatch size is 512 (i.e. when using the GPU), and to 10 if the minibatch size is 128 (i.e. when using the CPU). This makes sense since the quantity it is limiting is proportional to the number of samples in the minibatch.
The number of epochs that we train for is the sum of two configuration variables: –num-epochs (default: 15), and –num-epochs-extra (default: 5). The rule is that we train for –num-epochs epochs while reducing the learning rate geometrically from –initial-learning-rate to –final-learning-rate, and then keep it fixed at –final-learning rate, for –num-epochs-extra epochs. It's not generally necessary to change the number of epochs, except that sometimes for small databases we train for more epochs (20+5 instead of 15+5). Also, if the amount of data is very large, and particularly if your compute environmnt is not very high powered, you might want to train for fewer epochs by reducing these numbers, to save time. This may slightly degrade your final performance.
Something that is somewhat related to this is the parameter –num-iters-final. This determines the number of iterations over which we do the final model combination, at the end of training (see Final model combination). This is not a very critical parameter, we believe.
There is an option –splice-width, which defaults to 4, which controls how many frames we splice the input features over. This affects the initialization of the neural net, and also the generation of examples. The value of 4 means that we splice the input over 4 frames to the left and right of the central frame, or 9 frames in total. The –splice-width is actually a fairly critical parameter, but for normal "fully-processed" features (i.e. the 40-dimensional features derived from MFCC+splice+LDA+MLLT+fMLLR), 4 is normally an optimal value. Note that since the LDA+MLLT features are based on spliced frames with 3 or 4 frames on each side, this means that the total effective acoustic context that the neural net sees is 7 or 8 frames on each side. If instead of processed features like this you are using "raw" MFCC or log-filterbank-energy features (see the option "--feat-type raw" to get_egs.sh and get_lda.sh), then you might want to set the –splice-width a little higher, for example to 5 or 6.
Some people have asked us, "wouldn't it be better to use more temporal context than four frames?". The answer is, yes, it would be better if the goal were simply to get the best objective function or to classify isolated frames, or if you are decoding something like TIMIT in which there is no language model. The problem is that if you use too much context it can degrade the performance of the entire system. We believe the problem is that it interacts badly with the state-conditional frame independence assumption that HMMs are based on. Anyway, for whatever reason, it doesn't seem to work well.
We apply a decorrelating transform to the spliced features before training the neural network. This transform actually becomes part of the network– a component of type FixedAffineComponent that is fixed in advance and not trainable. We call it the "LDA transform" but it is not quite the same as conventional LDA because we apply a scaling to the rows of the transform. This section deals with the configuration values that affect that transorm. These need to be passed in to the program get_lda.sh by giving the option –lda-opts "<list of options>".
Note that apart from decorrelating the data, we also make it zero-mean; this is possible because the output is an affine transform (linear term plus bias), which is represented as d by (d+1) matrix rather than just d by d (where d is the feature dimension, typically 40 * 9). By default, this transform is a "non-dimension-reducing" form of LDA, i.e. we keep the full dimension. This may sound slightly strange, because normally the whole point of LDA is to reduce the dimensionality. But we are doing it as a way to decorrelated the data.
In conventional LDA, the way most people would code it, the data is normalized so that the within-class variance is the unit matrix, and the between-class variance is diagonalized with the diagonal of the between class variance ordered from largest to smallest. So after this transform, the total variance (within plus between-class) on the i'th diagonal is 1.0 + b(i), where b(i) is data-dependent, and decreases with i. Our modified LDA, which is not really LDA, takes this transform and multiplies each of the rows by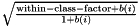 
, where by default within-class-factor is 0.0001. The effect on the variance of this is the square of this factor, so the effect is that the i'th element of the variance is not 1.0 + b(i), but 0.0001 + b(i), by default. Basically we are scaling down the dimensions that are "non-informative", since our experience is that adding non-informative data to the input of a neural net hurts performance, and simply by scaling it down we can make the SGD training ignore it for the most part, which is helpful. We suspect that if one made a simplifying assumption about the neural net, e.g. that it's just logistic regression or something similar, one could prove that a formula similar to this (maybe with a zero instead of 0.0001) would be somehow optimal. Anyway, for now it's just a hack.
There is a configuration parameter –lda-dim which can be used to force the transform to be dimension-reducing rather than passing all dimensions through. We have used this in the past when we were dealing with a setup where we felt the input dimension might be too high, but it wasn't clearly helpful.
For the train_tanh.sh, there is an option –shrink-interval (default: 5) that determines how often we do model "shrinking" (see Model "shrinking" and "fixing"), in which we use a small subset of training data to optimize a set of scales on the parameters of the different layers. This is not very critical.
The –add-layers-period option (default 2) controls how many iterations we wait between adding layers, at the start of training when we are adding new layers. This probably makes a difference but we dn't normally tune it.
We mentioned above that rather than using plain vanilla Stochastic Gradient Descent (SGD), we use a special preconditioned form of SGD. Basically this means that, instead of using a scalar learning rate, we use a matrix-valued learning rate. This matrix has a special structure, so in effect we have a matrix at the input dimension of each affine component, and one at the output dimension. If you want to view this as a single large matrix, it would have a block-diagonal structure where each block is a Kronecker product of two matrices (one for the input-dimension and one for the output-dimension of the corresponding affine component). In addition, this matrix is estimated per minibatch. The basic idea is to reduce the learning rate in dimensions where the derivatives have a high variance; this will tend to control instability and stop the parameters moving too fast in any one direction.
We don't have time at the moment to produce a detailed summary on this page, but see the comments in the source files nnet2/nnet-precondition.h and nnet2/nnet-precondition-online.h where this method is explained in detail. We should mention that nnet2/nnet-precondition.h contains the original, older version of this method, where the preconditioning matrix is estimated for each minibatch, and nnet2/nnet-precondition-online.h contains a newer version of this method, where the preconditioning matrix has a special low-rank plus unit-matrix structure and is estimated online; this is much more efficient for GPU implementation because the old method relied on symmetric matrix inversion that had to be done in relatively high dimension (e.g. 512), which is hard to do efficiently on a GPU and was becoming a bottleneck.
1.8.13