 |
|
The Kaldi matrix library is mostly a C++ wrapper for standard BLAS and LAPACK linear algebra routines.
This documentation page provides an overview of how to use the library. See Matrix and vector classes for code-level documentation, and see External matrix libraries for an explanation of how the matrix code makes use of external libraries.
The most important types defined by the matrix library are Matrix and Vector. We can illustrate their use with an example:
The code above first sets up v and w as vectors of size 10 and 9 respectively (the last element of v will be zero as the constructor sets the data to zero). The parenthesis operator indexes the vectors; a matrix would be indexed as M(i,j). M is initialized to a 10 x 9 matrix. The last line of the code adds the outer product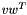 
to M. The naming scheme for the function is based on writing the operation as an equation, in this case:
![\[ M \leftarrow M + \alpha v w^T \]](form_23.png)
The "+" becomes "Add" in the name, and the types of the non-scalar arguments become parts of the name too, in this case "Vec" for v and "Vec" for w (so AddVecVec). The type of M doesn't appear here as the function is its class member.
Also notice that we correctly sized M before adding the outer product (we could have done this without using the constructor by calling Resize). The matrix library never tries to "guess" what size you want something to be, it will just crash if something is the wrong size. The only things that will resize a matrix are the constructor, Resize, and Read (and the assignment operator, which is mainly included so that we can declare std::vector<Matrix<double> > and the like).
To provide another example, if A, B and C are matrices and alpha and beta are scalars, to execute
![\[ A = \alpha B C^T + \beta A \]](form_24.png)
we would use the line of code
Here, kNoTrans and kTrans are enumeration values that indicate whether or not the matrix argument is transposed. An examples that illustrates this and some other issues is:
Note that in the BLAS tradition, there is no operation that does just, say,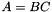 
; you have to use a special case of the example we just gave (e.g. with alpha=1 and beta=0).
To get an idea of what mathematical member functions are available in the Matrix and Vector classes, see the documentation for MatrixBase and VectorBase.
There are special types for symmetric matrices (SpMatrix) and triangular matrices (TpMatrix). These are both represented in memory as a "packed" lower-triangular matrix and both inherit from PackedMatrix. Of these, SpMatrix is the most useful (TpMatrix is mostly just used to compute Cholesky factors). A typical example of using these types is below. Notice the "AddMat2" function. This illustrates a new feature of our naming scheme: when a quantity appears twice in an expression we add "2" to the corresponding part of the function name.
This code would crash (cholesky.Invert() would throw an exception) if we did not initialize the features somehow where indicated.
For matrix operations that involve only part of a vector or matrix, the SubVector and SubMatrix classes are provided. Like Vector and Matrix, these inherit from VectorBase and MatrixBase respectively, so the implementation of operations that don't involve resizing is shared (you can never resize a SubVector or SubMatrix because it's treated as a pointer into the underlying Vector or Matrix).
An example of using these classes is here:
There are other ways to obtain these types. If M is a matrix, M.Row(3) will return row 3 of M, as a SubVector. There is a corresponding constructor, for example:
The same doesn't work for columns. This is because our vector types are contiguous in memory; we don't currently have a "stride" class-member (even though the underlying BLAS supports this). Another way to obtain these types is by using the Range functions of Vector and Matrix. For instance:
You have to be a little careful with SubVector and SubMatrix types. For instance, if you create a SubVector and then destroy or resize the underlying Vector or Matrix, the SubVector will be pointing to freed memory. Also, SubVector and SubMatrix do not respect const-ness the way they ideally should, so it is possible to modify a const Vector by creating a SubVector. Fixing these issues would have made the library a lot more complex.
In general, when a function requires a vector or matrix type, for greater flexibility we pass an argument of type e.g. VectorBase<BaseFloat> or MatrixBase<BaseFloat> rather than Vector<BaseFloat> or Matrix<BaseFloat>. That way the code is still callable if we are really passing a sub-matrix or sub-vector. The exception is where the code needs to resize the vector or matrix in question, in which case it would take a pointer of type e.g. Vector<BaseFloat>* or Matrix<BaseFloat>*; it cannot take a reference because resizing is non-const, and as per the style guide, functions cannot take non-const reference arguments.
There are different ways to copy vectors and matrices. The simplest ones are the CopyFrom functions, for instance Matrix::CopyFromMat, Vector::CopyFromVec, SpMatrix::CopyFromSp and so on. These will work even between float and double, unlike most of the mathematical operations. However, they will not resize the matrix for you and will crash if the sizes are wrong (you have to resize yourself using Vector::Resize, Matrix::Resize and so on). The same types of functions are available to copy between different matrix types, where this makes sense: for example, Matrix::CopyFromTp, SpMatrix::CopyFromMat, TpMatrix::CopyFromMat and so on. See the documentation of those functions for their exact behavior.
Wherever the above functions exist, corresponding constructors exist. These will do the copying but also resize, for instance:
There are also more special-purpose copying functions. You can copy the concatenated rows of a matrix to a vector (Vector::CopyRowsFromMat), the same for the columns (Vector::CopyColsFromMat), and do the reverse too (Matrix::CopyRowsFromVec and Matrix::CopyColsFromVec). The same functions exist for copying an individual row or column from a matrix to a vector and vice versa: see Vector::CopyRowFromMat, Vector::CopyColFromMat, Matrix::CopyRowFromVec and Matrix::CopyColFromVec. The row versions of these operations are only provided for symmetry, because you could do the same using SubVector in the row case (see Sub-vectors and sub-matrices.).
Various functions that return scalars (and do not modify their parameters) are defined not as class members but as functions. See Matrix-vector functions returning scalars for a list of these. Typical examples are:
All matrix and vector types (except for SubMatrix and SubVector) may be resized. Examples of this are below:
The Resize functions will set the new data to zero unless you provide an optional argument of type MatrixResizeType. The possible values are:
Thus, the code
will append a zero to v. This is not a particularly efficient way to append something to a list, though (it will newly allocate the whole array).
Constructors that take dimension arguments also optionally take a ResizeType argument (the default is kSetZero), so constructors behave in the same way as the Resize functions.
Matrix I/O is done in the same style as other Kaldi code (see Kaldi I/O mechanisms). A typical example of reading and writing these types is:
There also stream operators << and >> that do the same thing (in text mode only, not binary), but these are mainly intended for debugging. The text format of these objects looks like (for a vector):
and for a matrix:
This page is only a brief introduction to the matrix library. Most mathematical operations are members of the classes MatrixBase, VectorBase, SpMatrix and TpMatrix, and can be discovered there. Functions returning scalars are listed here. Some miscellaneous functions, including fourier transforms and the matrix exponential, are implemented as separate functions and classes and may be found here. We note that not all parts of the library have been optimized as fully as they could be. Our approach has been to quickly implement functionality that we need, and only optimize those parts that are taking a substantial amount of time in some scenario.
1.8.13